题目内容
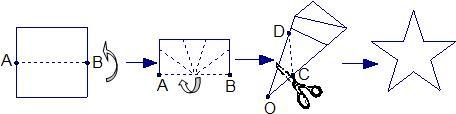
 如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为
如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为分析:根据折叠的性质可得BC是△ADE的中位线,则△ABC∽△ADE,相似比是
.即可求得△ABC与△ADE的面积,进而求解.
| 1 |
| 2 |
解答:解:∵△ABC≌△A′BC
∴B,C是△ADE的中位线.
∴△ABC∽△ADE,相似比是
.
∵△ABC的面积是
AB•AC=
×2×3=3.
∴△ADE的面积是3×4=12.
∴梯形BDEC的面积=△ADE的面积-△ABC的面积=12-3=9.
故答案为:9.
∴B,C是△ADE的中位线.
∴△ABC∽△ADE,相似比是
| 1 |
| 2 |
∵△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
∴△ADE的面积是3×4=12.
∴梯形BDEC的面积=△ADE的面积-△ABC的面积=12-3=9.
故答案为:9.
点评:本题主要考查了折叠的性质,正确理解BC是△ADE的中位线是解决本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

 沿
沿 折叠后,点
折叠后,点 、
、 分别落在
分别落在 、
、 的位置上,
的位置上, 交
交 于点
于点 .已知
.已知 ,那么
,那么 .
. 