题目内容
如图，一张矩形纸片ABCD的长AD=9cm，宽AB=3cm，现将其折叠，使点D与点B重合，则BE=5
5
．分析：连接BE，根据折叠的性质可知BE=ED，设BE=DE=x，则AE=AD-DE=8-x，然后根据勾股定理即可求得x的长．
解答：解：连接BE，
，
由折叠的性质可知：BE=ED，
设BE=DE=x，则AE=AD-DE=9-x，
∵ABCD为矩形，
∴∠A=90°，
在Rt△ABE中，BE2=AB2+AE2，即x2=（9-x）2+32，
解得：x=5，
即BE的长为5．
故答案为：5．
，由折叠的性质可知：BE=ED，
设BE=DE=x，则AE=AD-DE=9-x，
∵ABCD为矩形，
∴∠A=90°，
在Rt△ABE中，BE2=AB2+AE2，即x2=（9-x）2+32，
解得：x=5，
即BE的长为5．
故答案为：5．
点评：本题考查了翻折变换的知识，难度适中，解答本题的关键是根据勾股定理列出式子求得x的值．
练习册系列答案
相关题目
3、如图是一张矩形纸片ABCD，AD=10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=6cm，则CD=（ ）
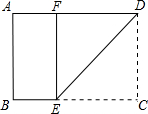如图是一张矩形纸片ABCD，AD=6cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=2cm，则DE=（ ）A、2
| ||
| B、4cm | ||
C、4
| ||
| D、6cm |
如图，一张矩形纸片沿BC折叠，顶点A落在点A′处，第二次过A′，再折叠，使折痕DE∥BC，若AB=2，AC=3，则梯形BDEC的面积为
（2012•高淳县一模）如图，一张矩形纸片ABCD中，AD＞AB．将矩形纸片ABCD沿过点A的直线折叠，使点D落到BC边上的点D′，折痕AE交DC于点E．