Question

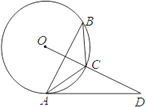
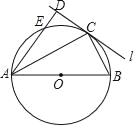
【题目】如图，AB为⊙O的直径，直线l经过⊙O上一点C，过点A作AD⊥l于点D，交⊙O于点E，AC平分∠DAB．

（1）求证：直线l是⊙O的切线；

（2）若DC＝4，DE＝2，求线段AB的长．

Answer 1

【答案】（1）详见解析；（2）AB＝10．

【解析】

（1）连接OC，由OA=OC可以得到∠OAC=∠OCA，然后利用角平分线的性质可以证明∠DAC=∠OCA；随之利用垂直即可解答.

(2) 连接BE交CO于M,得出四边形DEMC是矩形，利用勾股定理即可解答.

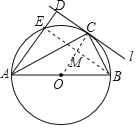
（1）证明：连接OC，

∵AC平分∠DAB，

∴∠DAC＝∠OAC，

又∵OA＝OC，

∴∠OCA＝∠OAC，

∴∠DAC＝∠OCA，

又∵CD⊥AD，即∠ADC＝90°，

∴∠DAC+∠DCA＝90°，

∴∠OCA+∠DCA＝90°，即∠OCD＝90°，

∴OC⊥CD，

则CD是圆O的切线；

（2）解：连接BE交CO于M，

∵AB为⊙O的直径，

∴∠AEB＝90°，

∴四边形DEMC是矩形，

∴OC⊥BE，

∴BM＝EM＝CD＝4，

在Rt△OMB中，BM2+OM2＝OB2，

∴42+（r﹣2）2＝r2，

∴r＝5，

∴AB＝10．