题目内容
9.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )| A. | 测量对角线是否相互平分 | B. | 测量两组对边是否分别相等 | ||
| C. | 测量对角线是否相等 | D. | 测量其中三个角是否都为直角 |
分析 根据矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线互相平分且相等的四边形是矩形.
解答 解:A、对角线是否相互平分,能判定平行四边形;
B、两组对边是否分别相等,能判定平行四边形;
C、对角线相等的四边形不一定是矩形,不能判定形状;
D、其中四边形中三个角都为直角,能判定矩形.
故选D.
点评 本题考查的是矩形的判定定理,牢记矩形的判定方法是解答本题的关键,难度较小.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
4.2015年3月份,苏州市某周的日最高气温统计如下表:则这七天中日最高气温的众数和中位数分别是( )
| 日期 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 最高气温/℃ | 2 | 4 | 5 | 3 | 4 | 6 | 7 |
| A. | 4,4 | B. | 5,4 | C. | 4,3 | D. | 4,4.5 |
14.-$\frac{1}{4}$的绝对值为( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
1. 2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )
2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )
 2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )
2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )| A. | 150$\sqrt{3}$米 | B. | 100$\sqrt{3}$米 | C. | (150$\sqrt{3}$-75)米 | D. | 50$\sqrt{3}$米 |
18. 如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )
如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )
 如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )
如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )| A. | (-2,0) | B. | (0,-2) | C. | (1,-1) | D. | (-1,1) |
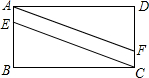 如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.
如图,在?ABCD中,E、F分别为边AB、CD上的点,且AE=$\frac{1}{5}$AB,CF=$\frac{1}{5}$CD,求证:四边形AECF是平行四边形.