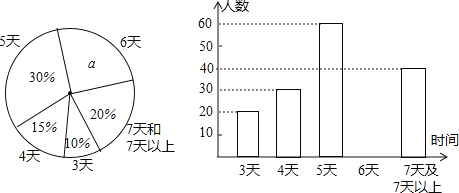
ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌ![]() ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЌЧвAЃЈЉ1ЃЌ0ЃЉЃЎ
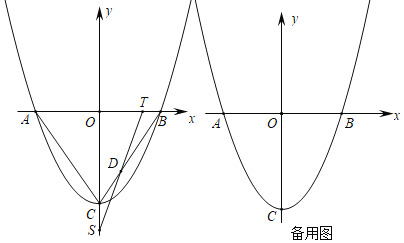
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
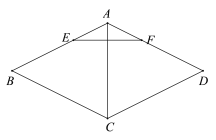
ЃЈ2ЃЉЕуPДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђЕуAдЫЖЏЃЌЭЌЪБЕуQДгЕуCГіЗЂЃЌвдУПУыvИіЕЅЮЛЕФЫйЖШЯђyжсИКЗНЯђдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЌСЌНгPQНЛЩфЯпBCгкЕуDЃЌЕБЕуPЕНДяЕуAЪБЃЌЕуQЭЃжЙдЫЖЏЃЌвдЕуPЮЊдВаФЃЌPBЮЊАыОЖЕФдВгыЩфЯпBCНЛгкЕуEЃЎ
ЂйЧѓBEЕФГЄЃЛЕБtЃН1ЪБЃЌЧѓDEЕФГЄЃЛ
ЂкШєдкЕуPЃЌQдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮDEЕФГЄЪМжеЪЧвЛИіЖЈжЕЃЌЧѓvЕФжЕМАDEГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2Љ
x2Љ![]() ЃЛЃЈ2ЃЉЂйЕБtЃН1ЪБЃЌ DEЃН1ЮЊЖЈжЕЃЛЂкдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН
ЃЛЃЈ2ЃЉЂйЕБtЃН1ЪБЃЌ DEЃН1ЮЊЖЈжЕЃЛЂкдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН![]() ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХзЮяЯпy=ax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌ-![]() ЃЉЃЌПЩЕУЖдГЦжсЃЌНЋХзЮяЯпНтЮіЪНИФЮЊЖЅЕуЪНЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыМДПЩЃЛ
ЃЉЃЌПЩЕУЖдГЦжсЃЌНЋХзЮяЯпНтЮіЪНИФЮЊЖЅЕуЪНЃЌНЋAЃЈ-1ЃЌ0ЃЉДњШыМДПЩЃЛ
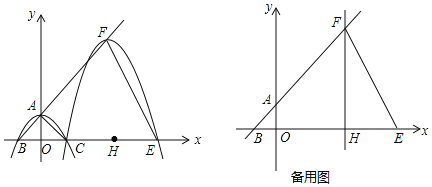
ЃЈ2ЃЉСЌНгPEЃЌЙ§DзїDЁЭyжсгкHЃЌЩшDH=aЃЌЩшОЙ§tУыЪБЃЌЂйЕБ0ЃМtЃМ1ЪБЃЌРћгУЁїQDHЁзЁїQPOМДПЩЕУDEЕФГЄгыtЮоЙиЃЌЮЊЖЈжЕЃЛЕБt=1ЪБЃЌвзЕУDE=CE=![]() BC=1ЮЊЖЈжЕЃЛЂкЕБ1ЃМtЁм2ЪБЃЌЁїQDHЁзЁїQPOЃЌПЩЕУDEЮЊЖЈжЕЃЎ
BC=1ЮЊЖЈжЕЃЛЂкЕБ1ЃМtЁм2ЪБЃЌЁїQDHЁзЁїQPOЃЌПЩЕУDEЮЊЖЈжЕЃЎ
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+cЕФЖЅЕуЮЊCЃЈ0ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЪЧyжсЃЌ
ЁрbЃН0ЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНax2Љ![]() ЃЌАбAЃЈЉ1ЃЌ0ЃЉДњШыyЃНax2Љ
ЃЌАбAЃЈЉ1ЃЌ0ЃЉДњШыyЃНax2Љ![]() ЃЌЕУaЃН
ЃЌЕУaЃН![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2Љ
x2Љ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНгPEЃЌЙ§DзїDЁЭyжсгкHЃЌЩшDHЃНaЃЌ
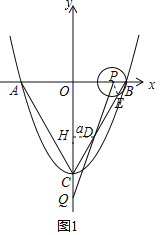
ЩшОЙ§tУыЪБЃЌPBЃНtЃЌCQЃНvtЃЌ
ЂйЕБ0ЃМtЃМ1ЪБЃЌ
ЁпPBЃНPEЃНtЃЌЁЯPBEЃН60ЁуЃЌ
ЁрЁїPBEЪЧЕШБпШ§НЧаЮЃЌ
ЁрBEЃНPBЃНtЃЛ
гж OPЃН1ЉtЃЌCQЃНvtЃЌQHЃНHC+CQЃНvt+![]() aЃЌQOЃНOC+CQЃНvt+
aЃЌQOЃНOC+CQЃНvt+![]() ЃЌ
ЃЌ
ЁпЁїQDHЁзЁїQPOЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ЁрDCЃН2DHЃН![]() ЃЌ
ЃЌ
ЁрDEЃНCBЉEBЉDCЃН2ЉtЉ![]() ЃН
ЃН![]() t+
t+![]() ЃЌ
ЃЌ
вРЬтвтЃЌDEЮЊЖЈжЕЃЌЙЪЕБvЃН![]() ЪБЃЌDEЕФГЄгыtЮоЙиЃЌМДDEЃН1ЃЛ
ЪБЃЌDEЕФГЄгыtЮоЙиЃЌМДDEЃН1ЃЛ
ЕБtЃН1ЪБЃЌPЕНOЕуЃЌCгыDжиКЯЃЌЯдШЛDEЃНCEЃН![]() BCЃН1ЮЊЖЈжЕЃЛ
BCЃН1ЮЊЖЈжЕЃЛ
ЂкШчЭМ2ЃЌЕБ1ЃМtЁм2ЪБЃЌOPЃНPBЉOBЃНtЉ1ЃЌ
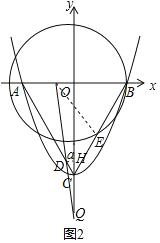
ЁпDHЃНaЃЌCHЃН![]() aЃЌQHЃНCQЉCHЃНvtЉ
aЃЌQHЃНCQЉCHЃНvtЉ![]() aЃЌQOЃНCQ+OCЃНvt+
aЃЌQOЃНCQ+OCЃНvt+![]() ЃЌ
ЃЌ
ЭЌРэЃЌЁїQDHЁзЁїQPOЃЌЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ЁрDCЃН2DHЃН![]() ЃЌ
ЃЌ
ЁрDEЃНDC+CEЃН![]() +ЃЈ2ЉtЃЉЃН
+ЃЈ2ЉtЃЉЃН![]() t+
t+![]() ЃЌ
ЃЌ
вРЬтвтЃЌDEЮЊЖЈжЕЃЌЙЪЕБvЃН![]() ЪБЃЌDEЃН1ЃЌ
ЪБЃЌDEЃН1ЃЌ
злЩЯЫљЪіЃЌдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌvЃН![]() ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ
ЃЌЯпЖЮDEЕФГЄЪЧЖЈжЕ1ЃЎ