题目内容
20. 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC于点E,DM=DN,若△AMD的面积为100,△AND的面积为80;则△DEN的面积为10.
如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC于点E,DM=DN,若△AMD的面积为100,△AND的面积为80;则△DEN的面积为10.
分析 由AD是∠BAC的平分线,得到∠DAP=∠DAN,推出△APD≌△AND,得到PD=ND,等量代换即可得到结论,过D作DG⊥AB于G,根据角平分线的性质得到DE=DG,证得△DEN≌△DPG,由已知条件得到△DPM的面积等于20,根据等腰三角形的性质得到PG=$\frac{1}{2}$PM,于是得到结果.
解答 解:在AM上截取AP=AN,连接DP,过D作DG⊥AB于G,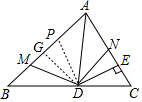
∵AD是∠BAC的平分线,
∴∠DAP=∠DAN,
在△APD与△AND中,
$\left\{\begin{array}{l}{AP=AN}\\{∠PAD=∠NAD}\\{AD=AD}\end{array}\right.$,
∴△APD≌△AND,
∴PD=ND,
∵DM=DN,
∴DP=DM,
∵DG⊥AB,DE⊥AC,AD是∠BAC的平分线,DH⊥AC,
∴DH=DG,
在Rt△DEN与Rt△DPG中,
$\left\{\begin{array}{l}{DN=DP}\\{DE=DG}\end{array}\right.$,
∴Rt△DEN≌Rt△DPG
∵△AMD的面积等于100,△AND的面积等于80,
∴△DPM的面积等于20,
∵DP=DM,DG⊥PM,
∴PG=$\frac{1}{2}$PM,
∴△DEN的面积=△DPG的面积=$\frac{1}{2}$△DPM的面积=10,
故答案为:10.
点评 本题考查了角平分线的性质,等腰三角形的性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.若(x+1)2+|y-2017|=0,则2017-xy的值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |

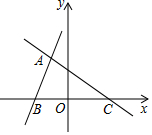 如图,直线AB的解析式为y1=k1x+b1,直线AC解析式为y2=k2x+b2,它们分别与x轴交于点B、C,且B、A、C三点的横坐标分别为-2,-1,2,则满足y1>y2>0的x的取值范围是-1<x<2.
如图,直线AB的解析式为y1=k1x+b1,直线AC解析式为y2=k2x+b2,它们分别与x轴交于点B、C,且B、A、C三点的横坐标分别为-2,-1,2,则满足y1>y2>0的x的取值范围是-1<x<2.