题目内容
已知函数y=x2+2x+4上的三点(-2015,y1),(2014,y2),(2015,y3),则下列选项正确的是( )
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y2<y3<y1 |
| D、y3<y1<y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:根据抛物线解析式求得抛物线顶点坐标,利用抛物线的增减性比较它们的大小.
解答:解:∵y=x2+2x+4=(x+1)2+3,
∴该抛物线的顶点坐标是(-1,3).
∵该抛物线的开口方向上,
∴当x<-1时,y随x的增大而减小,当x>-1时,y随x的增大而增大.
∵|-2015-(-1)|<|2014-(-1)|,2014<2015
∴y1<y2,y2<y3,
∴y1<y2<y3.
故选:A.
∴该抛物线的顶点坐标是(-1,3).
∵该抛物线的开口方向上,
∴当x<-1时,y随x的增大而减小,当x>-1时,y随x的增大而增大.
∵|-2015-(-1)|<|2014-(-1)|,2014<2015
∴y1<y2,y2<y3,
∴y1<y2<y3.
故选:A.
点评:本题考查了二次函数图象上点的坐标特征.解题时,利用了抛物线的增减性.

练习册系列答案
相关题目
 如图,是一个圆柱体笔筒和一个正方体箱子,那么它的主视图是( )
如图,是一个圆柱体笔筒和一个正方体箱子,那么它的主视图是( )A、 |
B、 |
C、 |
D、 |
若
在实数范围内有意义,则x的取值范围是( )
| x-3 |
| A、x>0 | B、x>3 |
| C、x≤3 | D、x≥3 |
方程x2=x的解是( )
| A、0 | B、1 | C、无解 | D、0和1 |
 如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF=
如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF= 如图,已知△ABC≌△AFE,若∠ACB=65°,则∠EAC等于
如图,已知△ABC≌△AFE,若∠ACB=65°,则∠EAC等于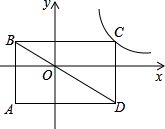 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 求阴影部分面积:
求阴影部分面积: