题目内容
若有理数数x，y满足xy≠0，则m=
+
的最大值是
| x |
| |x| |
| |y| |
| y |
2
2
．分析：首先根据绝对值的定义去掉绝对值符号，然后注意讨论结果有正负之分．
解答：解：∵有理数x，y满足xy≠0，
∴
=±1，
=±1，
∴m=
+
的最大值是m=1+1=2．
故答案为：2．
∴
| x |
| |x| |
| |y| |
| y |
∴m=
| x |
| |x| |
| |y| |
| y |
故答案为：2．
点评：本题主要考查了实数的运算和绝对值的定义，也同时考查分类讨论思想．
练习册系列答案
名校课堂系列答案
相关题目
的最大值是________．
，再减去余下的
，再减去余下的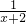
，再减去余下的
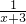，再减去余下的
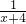，依此类推，直到最后减去余下的
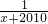，求最后所得结果．