题目内容
(1997•浙江)开口向下的抛物线y=a(x+1)(x-9)与x轴交于点A,B,与y轴交于点C,若∠ACB=90°,则a的值是
-
| 1 |
| 3 |
-
.| 1 |
| 3 |
分析:根据抛物线解析式y=a(x+1)(x-9)可知A、B两点的坐标分别为(-1,0)和(9,0).而抛物线与y轴交点C处,可令x=0,得到y=-9a.即C点的坐标为(0,-9a),其中a小于0.然后利用勾股定理列出关于a的方程,通过解方程求得a的值.
解答: 解:∵抛物线y=a(x+1)(x-9)的开口向下,
解:∵抛物线y=a(x+1)(x-9)的开口向下,
∴a<0.
又∵抛物线解析式是y=a(x+1)(x-9),
∴A(-1,0)、B(9,0).
令x=0,则y=-9a,
∴C(0,-9a).
∵∠ACB=90°,
∴AC2+BC2=AB2,即1+81a2+81+81a2=100,
解得a=
(不合题意,舍去),或x=-
.
故答案是:-
.
 解:∵抛物线y=a(x+1)(x-9)的开口向下,
解:∵抛物线y=a(x+1)(x-9)的开口向下,∴a<0.
又∵抛物线解析式是y=a(x+1)(x-9),
∴A(-1,0)、B(9,0).
令x=0,则y=-9a,
∴C(0,-9a).
∵∠ACB=90°,
∴AC2+BC2=AB2,即1+81a2+81+81a2=100,
解得a=
| 1 |
| 3 |
| 1 |
| 3 |
故答案是:-
| 1 |
| 3 |
点评:本题考查了抛物线的与x轴的交点.求a的值时,也可以在直角△ACB中利用射影定理列出关于a的方程.

练习册系列答案
相关题目
抛物线y=-x2+2x+1,它的( )
| A、开口向上,最大值是2 | B、开口向下,最小值是2 | C、开口向上,最小值是2 | D、开口向下,最大值是2 |
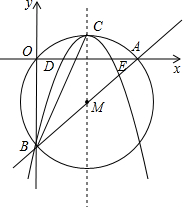 线上是否存在点P,使△PDE的面积是△ABC面积的
线上是否存在点P,使△PDE的面积是△ABC面积的