��Ŀ����
��ͼ��ʾ����ƽ��ֱ������ϵ�У�������ԭ��O��ԲM�ֱ�x�ᡢy���ڵ�A��6��0����B��0��-8������1����ֱ��AB�Ľ���ʽ��
��2������һ�������ߵĶԳ���ƽ����y���Ҿ���M�㣬����C��ԲM�ϣ��������£��Ҿ�����B����������ߵĽ���ʽ��
��3���裨2���е���������x�ύ��D��x1��y1����E��x2��y2�����㣬��x1��x2��������
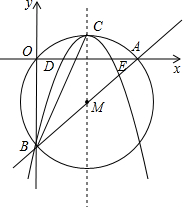 �����Ƿ���ڵ�P��ʹ��PDE������ǡ�ABC�����
�����Ƿ���ڵ�P��ʹ��PDE������ǡ�ABC�����| 1 | 5 |
��������1����֪��A��B��������꣬���ô���ϵ�������ֱ��AB�Ľ���ʽ��
��2����֪��A��B�����꣬M���߶�AB���е㣬���ѵó�M��������Բ�İ뾶���ݴ˿����C������꣮Ȼ���ö���ʽ���κ�������ʽ�������ߣ���B��������������ߵĽ���ʽ�м����������ϵ����ֵ��Ҳ�͵ó��������ߵĽ���ʽ��
��3�������������ABC��������ɽ�������ABC�ֳ�������AMC��������BMC����������Ȼ�����������ABC��������PDE����������������PDE�����������������PDE�У�DE�ij��Ƕ�ֵ����˿����P���������ľ���ֵ��������������ߵĽ���ʽ�м������P�����꣮
��2����֪��A��B�����꣬M���߶�AB���е㣬���ѵó�M��������Բ�İ뾶���ݴ˿����C������꣮Ȼ���ö���ʽ���κ�������ʽ�������ߣ���B��������������ߵĽ���ʽ�м����������ϵ����ֵ��Ҳ�͵ó��������ߵĽ���ʽ��
��3�������������ABC��������ɽ�������ABC�ֳ�������AMC��������BMC����������Ȼ�����������ABC��������PDE����������������PDE�����������������PDE�У�DE�ij��Ƕ�ֵ����˿����P���������ľ���ֵ��������������ߵĽ���ʽ�м������P�����꣮
����⣺��1����ֱ��AB�Ľ���ʽΪy=kx+b
�������⣬�ã�
��֮����k=
��b=-8
��ֱ��AB�Ľ���ʽΪy=
x-8
��2���������߶Գ��ύx����F��
�ߡ�AOB=90�㣬
��ABΪԲM��ֱ������AM=BM��
�������ߵĶԳ��ᾭ����M������y��ƽ�У�OA=6��
��Գ��᷽��Ϊx=3��
���Գ��ύԲM��C��
��MF�ǡ�AOB����λ�ߣ�
��MF=
BO=4��
��CF=CM-MF=1��
�ߵ�C��3��1�����������֪C��3��1���������������ߵĶ��㣮
����һ���������߽���ʽΪy=a��x-3��2+1��
�������߹���B��0��-8����
��-8=a��0-3��2+1��
��ã�a=-1��
�������ߵĽ���ʽΪy=-��x-3��2+1��y=-x2+6x-8��
���������������߹���B��0��-8����
����������ߵĽ���ʽΪy=ax2+bx-8��
������ɵã�
��
��a=-1��b=6��
�������ߵĽ���ʽΪy=-x2+6x-8��
��3����-x2+6x-8=0����x1=2��x2=4��
��D��2��0����E��4��0����
��P��x��y����
��S��PDE=
•DE•|y|=
��2|y|=|y|��
S��ABC=S��BCM+S��ACM=
•CM•��3+3��=
��5��6=15��
�����������ĵ�P������|y|=
��15=3��
�Ӷ�y=��3��
��y=3ʱ��-x2+6x-8=3��
�����ã�x2-6x+11=0��
�ߡ�=��-6��2-4��11��0��
��˷�����ʵ������
��y=-3ʱ��-x2+6x-8=-3��
�����ã�x2-6x+5=0��
��ã�x1=1��x2=5��
��������P����ڣ��������������ĵ㣺P1��1��-3����P2��5��-3����
�������⣬�ã�
|
��֮����k=
| 4 |
| 3 |

��ֱ��AB�Ľ���ʽΪy=
| 4 |
| 3 |
��2���������߶Գ��ύx����F��
�ߡ�AOB=90�㣬
��ABΪԲM��ֱ������AM=BM��
�������ߵĶԳ��ᾭ����M������y��ƽ�У�OA=6��
��Գ��᷽��Ϊx=3��
���Գ��ύԲM��C��
��MF�ǡ�AOB����λ�ߣ�
��MF=
| 1 |
| 2 |
��CF=CM-MF=1��
�ߵ�C��3��1�����������֪C��3��1���������������ߵĶ��㣮
����һ���������߽���ʽΪy=a��x-3��2+1��
�������߹���B��0��-8����
��-8=a��0-3��2+1��
��ã�a=-1��
�������ߵĽ���ʽΪy=-��x-3��2+1��y=-x2+6x-8��
���������������߹���B��0��-8����
����������ߵĽ���ʽΪy=ax2+bx-8��
������ɵã�
|
��a=-1��b=6��
�������ߵĽ���ʽΪy=-x2+6x-8��
��3����-x2+6x-8=0����x1=2��x2=4��
��D��2��0����E��4��0����
��P��x��y����
��S��PDE=
| 1 |
| 2 |
| 1 |
| 2 |
S��ABC=S��BCM+S��ACM=
| 1 |
| 2 |
| 1 |
| 2 |
�����������ĵ�P������|y|=
| 1 |
| 5 |
�Ӷ�y=��3��
��y=3ʱ��-x2+6x-8=3��
�����ã�x2-6x+11=0��
�ߡ�=��-6��2-4��11��0��
��˷�����ʵ������
��y=-3ʱ��-x2+6x-8=-3��
�����ã�x2-6x+5=0��
��ã�x1=1��x2=5��
��������P����ڣ��������������ĵ㣺P1��1��-3����P2��5��-3����
���������⿼����һ�κ�������κ�������ʽ��ȷ��������ͼ�㡢ͼ���������֪ʶ�㣮�ۺ��Խ�ǿ���Ѷ����У�

��ϰ��ϵ�д�
�����Ŀ
 ���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ��
���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ�� 5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������
5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������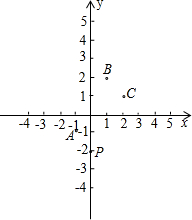 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ�� ��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ
��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ BE��
BE��