��Ŀ����
��֪��ֱ��������AOB�У���AOB=90�㣬OA=3���ף�OB=4���ף���OΪ����ԭ����ͼ����ƽ��ֱ������ϵ����P��Q�ֱ�ΪAB�ߣ�OB���ϵĶ��㣬����ͬʱ�ֱ�ӵ�A��O��B�������˶����ƶ����ٶȶ�Ϊ1����ÿ�룮��P��Q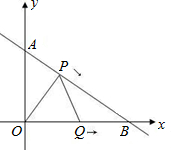 �˶���ʱ��Ϊt�루0��t��4����
�˶���ʱ��Ϊt�루0��t��4������1�����OPQ�����S�루����2����t�ĺ�����ϵʽ����ָ����tΪ��ֵʱS�����ֵ�Ƕ��٣�
��2����tΪ��ֵʱ����BPQ�͡�AOB���ƣ�
��3����tΪ��ֵʱ����OPQΪֱ�������Σ�
��4������֤������tΪ��ֵ����OPQ������Ϊ�������Σ�
������P���ƶ��ٶȲ��䣬�Ըı��Q���˶��ٶȣ�ʹ��OPQΪ�������Σ������Q���˶��ٶȺʹ�ʱ��tֵ��
��������1������t��ʾ��OQ��BP�ij���������OPQ�У�OQ���ϵĸ߿���BP�ij��͡�PBO������ֵ������ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
��2����������������
�١�BQP=��BOA����ʱPQ��OA����ôBQ=PB•cos��PBO���ɴ˿����t��ֵ��
�ڡ�BPQ=��BOA����ʱBP=BQ•sin��PBO���ɴ˿����t��ֵ��
��3�������������������OQ��PQ��OP��QP���ɷֱ��ʾ��PO��QO��PQ�����߶εij���Ȼ���ù��ɶ���������⼴�ɣ�
��4�������������OPQ������������ô��3���б�ʾ�����߶γ��ı���ʽ��Ȼ��ȣ���ͨ���ⷽ�������ʱt��ֵ�������������˵��������OPQ���������������Σ�
��˼·ͬ�٣����Q����ٶȣ�Ȼ���ʾ�������߶εij����������߶εı���ʽ��ȣ��������Q���ٶȺ�t��ֵ��
��2����������������
�١�BQP=��BOA����ʱPQ��OA����ôBQ=PB•cos��PBO���ɴ˿����t��ֵ��
�ڡ�BPQ=��BOA����ʱBP=BQ•sin��PBO���ɴ˿����t��ֵ��
��3�������������������OQ��PQ��OP��QP���ɷֱ��ʾ��PO��QO��PQ�����߶εij���Ȼ���ù��ɶ���������⼴�ɣ�
��4�������������OPQ������������ô��3���б�ʾ�����߶γ��ı���ʽ��Ȼ��ȣ���ͨ���ⷽ�������ʱt��ֵ�������������˵��������OPQ���������������Σ�
��˼·ͬ�٣����Q����ٶȣ�Ȼ���ʾ�������߶εij����������߶εı���ʽ��ȣ��������Q���ٶȺ�t��ֵ��
����⣺��1��S=-0.3t2+
t��t=
ʱ��S���=
��
��2���١�BQP=��BOA����ֱ��������BQP�У�BP=
BQ��
��5-t=
��4-t����
���t=0��
�ڡ�BPQ=��BOA����ֱ��������BPQ�У�BQ=
BP��
��4-t=
��5-t����
���t=9��
��Ϊ0��t��4��
��t=9�������⣬��ȥ��
��˵�t=0ʱ����BPQ�͡�AOB���ƣ�
��3������OPQΪֱ�������Σ���OQ��PQ��OP��QP����QP��OQ��
��PQ=
=
=
��
PO=
=
=
��
OQ=
=
=
��t��t�⣩��
��QP����OQ��ֱ
��OP��QP�����OPQ�ס�PNQ
��
=
��
=
��PQ2=
t2��PQ2=OQ2-OP2=t2-t2+
t-9=
t-9
t2=
t-9��
���t=3��t=15������������ȥ��
�൱t=3�ǡ�OPQ��ֱ�������Σ�
��4����PO=
��OQ=t��PQ=
��PO=OQ=PQ����t��
���OPQ���ܳ�Ϊ�������Σ�
����Q���ٶ�Ϊx����OQ=xt��
OP2=t2-
t+9��OQ2=x2t2��PQ2=
t2-
t+12
��OP2=OQ2=PQ2
���x=
��t=
��ȥ��ֵ����t=
���Q����ٶ�Ϊ
��
t=
��
| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
| 8 |
��2���١�BQP=��BOA����ֱ��������BQP�У�BP=
| 4 |
| 5 |
��5-t=
| 4 |
| 5 |
���t=0��
�ڡ�BPQ=��BOA����ֱ��������BPQ�У�BQ=
| 4 |
| 5 |
��4-t=
| 4 |
| 5 |
���t=9��
��Ϊ0��t��4��
��t=9�������⣬��ȥ��
��˵�t=0ʱ����BPQ�͡�AOB���ƣ�
��3������OPQΪֱ�������Σ���OQ��PQ��OP��QP����QP��OQ��
��PQ=
| PB2-QB2 |
=
| (5-t)2-(4-t)2 |
=
| 9-2t |
PO=
| PM2+OM2 |
=
(
|
=
t2-
|
OQ=
| OP2-PQ2 |
=
t2-
|
=
t2-
|
��QP����OQ��ֱ
��OP��QP�����OPQ�ס�PNQ
��
| NQ |
| PQ |
| PQ |
| OQ |
| ||
| PQ |
| PQ |
| t |
��PQ2=
| 1 |
| 5 |
| 18 |
| 5 |
| 18 |
| 5 |
| 1 |
| 5 |
| 18 |
| 5 |
���t=3��t=15������������ȥ��
�൱t=3�ǡ�OPQ��ֱ�������Σ�
��4����PO=
t2-
|
(
|
��PO=OQ=PQ����t��
���OPQ���ܳ�Ϊ�������Σ�
����Q���ٶ�Ϊx����OQ=xt��
OP2=t2-
| 18 |
| 5 |
| 15 |
| 25 |
| 24 |
| 5 |
��OP2=OQ2=PQ2
���x=
| 8 |
| 5 |
-15��20
| ||
| 13 |
��ȥ��ֵ����t=
20
| ||
| 13 |
���Q����ٶ�Ϊ
| 8 |
| 5 |
t=
20
| ||
| 13 |
���������⿼����κ������ۺ�Ӧ�ã������漰����֪ʶ���д���ϵ������������ʽ�͵������Σ�Բ���й����ʵȣ�Ҫ�������ղ���������ã�

��ϰ��ϵ�д�
�����Ŀ
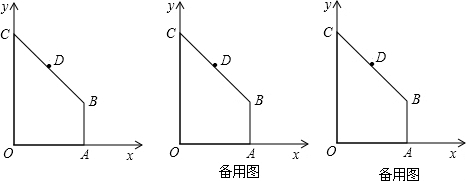
 ��2013•��ͨһģ����֪����ͼ��ֱy=2x+b��x���ڵ�B����y���ڵ�C����AΪx����������һ�㣬AO=CO����ABC�����Ϊ12��
��2013•��ͨһģ����֪����ͼ��ֱy=2x+b��x���ڵ�B����y���ڵ�C����AΪx����������һ�㣬AO=CO����ABC�����Ϊ12�� ��ͼ����֪B��0��4������A�ڵ�һ���ޣ���AB��y�ᣬ��A=30�㣮
��ͼ����֪B��0��4������A�ڵ�һ���ޣ���AB��y�ᣬ��A=30�㣮