题目内容
已知等腰直角三角形ABC的底边为AB,直线l过直角顶点C,分别过点A、B作l的垂线,垂足分别为E、F.
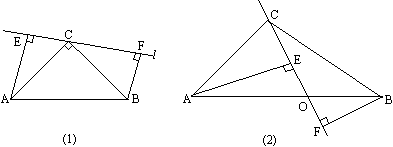
(1)如图(1),当l与AB不相交时,求证:EF=AE+BF
(2)如图(2),当l与AB相交于O,且AO>BO,其他条件不变,请猜想EF、AE、BF间的等量关系,并证明.
答案:
解析:
解析:
|
(1)∵∠E=∠F= ∠ EAC+∠ECA=∠ ECA+∠BCF=∴∠ EAC=∠BCF.AC=BC∴ Rt△ACE≌Rt△CBF(AAS)∴ EC=BF,AE=CF∴ EF=EC+CF=AE+BF.(2)同理可证Rt△ACE≌Rt△CBF ∴ EC=BF,AE=CF又 EF=CF-CE=AE-BF. |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知等腰直角三角形外接圆半径为5,则内切圆半径为( )
A、5
| ||
B、12
| ||
C、5
| ||
D、10
|
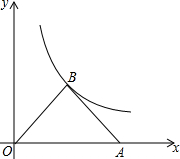 如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线
如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线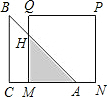 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合,求重叠部分的面积ycm2与时间ts之间的函数关系式.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合,求重叠部分的面积ycm2与时间ts之间的函数关系式.