题目内容
 (2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.
(2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.(1)求证:△PAD∽△ABC;
(2)若PA=10,AD=6,求AB和PE的长.
分析:(1)由PA为圆O的切线,利用切线的性质得到AP垂直于AB,可得出∠PAO为直角,得到∠PAD与∠DAO互余,再由AB为圆O的直径,根据直径所对的圆周角为直角,可得出∠ACB为直角,得到∠DAO与∠B互余,根据同角的余角相等可得出∠PAC=∠B,再由一对直角相等,利用两对对应角相等的两三角形相似可得出三角形APD与三角形ABC相似;
(2)在直角三角形APD中,利用勾股定理求出PD的长,进而确定出AC的长,由第一问两三角形相似得到的比例式,将各自的值代入求出AB的上,求出半径AO的长,在直角三角形APO中,由AP及AO的长,利用勾股定理求出OP的长,用OP-OE即可求出PE的长.
(2)在直角三角形APD中,利用勾股定理求出PD的长,进而确定出AC的长,由第一问两三角形相似得到的比例式,将各自的值代入求出AB的上,求出半径AO的长,在直角三角形APO中,由AP及AO的长,利用勾股定理求出OP的长,用OP-OE即可求出PE的长.
解答:(1)证明:∵PA是⊙O的切线,AB是直径,
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC;
(2)解:∵∠PAO=90°,PA=10,AD=6,
∴PD=
=8,
∵OD⊥AC,
∴AD=DC=6,
∴AC=12,
∵△PAD∽△ABC,
∴
=
,
∴
=
,
∴AB=15,
∴OE=
AB=
,
∵OP=
=
,
∴PE=OP-OE=
-
=5.
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B,
又∵OP⊥AC,
∴∠ADP=∠C=90°,
∴△PAD∽△ABC;
(2)解:∵∠PAO=90°,PA=10,AD=6,
∴PD=
| PA2-AD2 |
∵OD⊥AC,
∴AD=DC=6,

∴AC=12,
∵△PAD∽△ABC,
∴
| AP |
| AB |
| PD |
| AC |
∴
| 10 |
| AB |
| 8 |
| 12 |
∴AB=15,
∴OE=
| 1 |
| 2 |
| 15 |
| 2 |
∵OP=
| AO2+AP2 |
| 25 |
| 2 |
∴PE=OP-OE=
| 25 |
| 2 |
| 15 |
| 2 |
点评:此题考查了切线的性质,相似三角形的判定与性质,圆周角定理,勾股定理,垂径定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
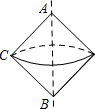 (2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2
(2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2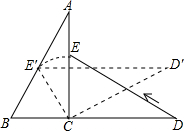 (2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,
(2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,
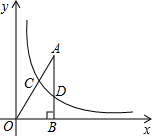 (2013•沙市区一模)如图,已知点A的坐标为(
(2013•沙市区一模)如图,已知点A的坐标为(