题目内容
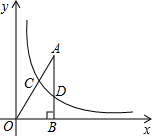 (2013•沙市区一模)如图,已知点A的坐标为(
(2013•沙市区一模)如图,已知点A的坐标为(| 3 |
| k |
| x |
2+
| ||
| 2 |
2+
| ||
| 2 |
分析:连接CD,作CE⊥x轴于E,由于点A的坐标为(
,3),AB=3BD,D点坐标为(
,1),得到k=
,再利用待定系数法求出直线OA的解析式为y=
x,然后解方程组
得C点坐标为(1,
),再利用四边形BOCD的面积=S△OCD+S梯形CEBD进行计算即可.
| 3 |
| 3 |
| 3 |
| 3 |
|
| 3 |
解答: 解:连接CD,作CE⊥x轴于E,如图
解:连接CD,作CE⊥x轴于E,如图
∵点A的坐标为(
,3),AB=3BD,
∴D点坐标为(
,1),
∴k=
×1=
设直线OA的解析式为y=kx,把A(
,3)代入得3=
k,解得k=
,
∴直线OA的解析式为y=
x,
解方程组
得
或
,
∴C点坐标为(1,
),
∴四边形BOCD的面积=S△OCE+S梯形CEBD=
+
(1+
)×(
-1)=
.
故答案为:
.
 解:连接CD,作CE⊥x轴于E,如图
解:连接CD,作CE⊥x轴于E,如图∵点A的坐标为(
| 3 |
∴D点坐标为(
| 3 |
∴k=
| 3 |
| 3 |
设直线OA的解析式为y=kx,把A(
| 3 |
| 3 |
| 3 |
∴直线OA的解析式为y=
| 3 |
解方程组
|
|
|
∴C点坐标为(1,
| 3 |
∴四边形BOCD的面积=S△OCE+S梯形CEBD=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
2+
| ||
| 2 |
故答案为:
2+
| ||
| 2 |
点评:本题考查了反比例函数y=
(k≠0)的k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
| k |
| x |

练习册系列答案
相关题目
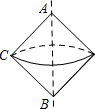 (2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2
(2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2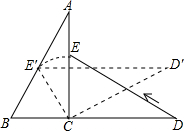 (2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,
(2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,