题目内容
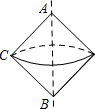 (2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2
(2013•沙市区一模)如图,Rt△ABC中,∠ACB=90°,AC=BC=2| 2 |
8
π
| 2 |
8
π
.| 2 |
分析:首先求得高CD的长,然后根据圆锥的侧面积的计算方法,即可求解.
解答: 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
Rt△ABC中,∠ACB=90°,AC=BC,
∴AB=
AC=4,
∴CD=2,
以CD为半径的圆的弧长是:4π.
故直线旋转一周则所得的几何体得表面积是:2×
×4π×2
=8
π.
故答案为:8
π.
 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,Rt△ABC中,∠ACB=90°,AC=BC,
∴AB=
| 2 |
∴CD=2,
以CD为半径的圆的弧长是:4π.
故直线旋转一周则所得的几何体得表面积是:2×
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:8
| 2 |
点评:此题主要考查了圆锥的有关计算,正确确定旋转后的图形得出以CD为半径的圆的弧长是解题的关键.

练习册系列答案
相关题目
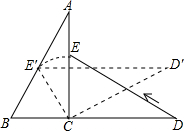 (2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,
(2013•沙市区一模)两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB边上的E′点时,
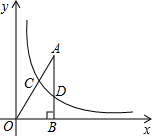 (2013•沙市区一模)如图,已知点A的坐标为(
(2013•沙市区一模)如图,已知点A的坐标为(