题目内容
20．
如图，圆O是△ACD的外接圆，AB是圆O的直径，∠BAD=60°，则∠C的度数是（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
分析 先根据直径所对的圆周角为直角得到∠ADB=90°，再利用三角形内角和定理可计算出∠B=40°，然后根据圆周角定理即可得到∠C的度数．
解答 解：∵AB为⊙O的直径，
∴∠ADB=90°，
∴∠B=180°-∠ADB-∠BAD=180°-90°-60°=30°，
∴∠C=∠B=30°．
故选：A．
点评 本题考查了圆周角定理及其推论：在同圆或等圆中，同弧或等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半；直径所对的圆周角为直角．
练习册系列答案
相关题目
10．-4的倒数是（ ）
| A． | 4 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | 16 |
11．若（a+1）2+|2-b|=0，则ba的值为（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
8．某棉纺厂为了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x（单位：mm）的数据分布如下表，则棉花纤维长度的数据在8≤x＜32这个范围的频率为0.8．
| 棉花纤维长度x | 频数 |
| 0≤x＜8 | 1 |
| 8≤x＜16 | 2 |
| 16≤x＜24 | 8 |
| 24≤x＜32 | 6 |
| 32≤x＜40 | 3 |
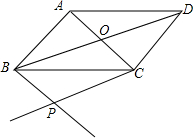如图，?ABCD的对角线AC，BD相交于点O，过点B作BP∥AC，过点C作CP∥BD，BP与CP相交于点P，试判断四边形BPCO的形状，并说明理由．