题目内容
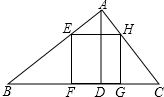如图，已知在△ABC中，AD是高，EFGH是△ABC的内接矩形，其中点E，H分别在AB，AC上，点F，G在BC上．若BC=6，AD=3．（1）设EF=x，EH=y，求y与x的函数关系式，并求自变量x的取值范围；
（2）设EF=x，四边形EFGH的面积为S，求S与x的函数关系式，并求当x取何值时，S有最大值，最大值是多少？
考点：相似三角形的判定与性质,二次函数的最值
专题：
分析：（1）设EF=x，EH=y，根据EH∥BC，可得
=
，代入EH，AM长度即可解题；
（2）根据（1）中结论可以得出EH和EF的关系，即可求得S关于x的二次函数式，根据二次函数的最值问题即可解题．
| EH |
| BC |
| AM |
| AD |
（2）根据（1）中结论可以得出EH和EF的关系，即可求得S关于x的二次函数式，根据二次函数的最值问题即可解题．
解答：解：（1）设EF=x，EH=y，
则DM=EF=x，AM=AD-DM=3-x，
∵EH∥BC，
∴
=
，即
=
，
∴y=6-2x；
∵y＞0，∴6-2x＞0，即x＜3，
∵x＞0，∴x取值范围为0＜x＜3；
（2）设EF=x，四边形EFGH的面积为S，
则S=x（6-2x）=-2x2+6x，
在x=
=
时，S有最大值为
．
则DM=EF=x，AM=AD-DM=3-x，
∵EH∥BC，
∴
| EH |
| BC |
| AM |
| AD |
| y |
| 6 |
| 3-x |
| 3 |
∴y=6-2x；
∵y＞0，∴6-2x＞0，即x＜3，
∵x＞0，∴x取值范围为0＜x＜3；
（2）设EF=x，四边形EFGH的面积为S，
则S=x（6-2x）=-2x2+6x，
在x=
| 6 |
| 2×2 |
| 3 |
| 2 |
| 9 |
| 2 |
点评：本题考查了平行线对应线段成比例的性质，考查了二次函数的最值问题，本题中列出S关于x的函数式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，DE⊥BC，BC=40，CD=10，DE=20，则AC的长为
如图所示，直线PD为△ABC一边BC的垂直平分线，点D为垂足，连接CP并延长CP交边AB于点F，射线BP交边AC于点E．