题目内容
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
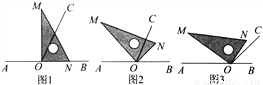
(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=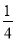 ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
练习册系列答案
相关题目
题目内容
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;

(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=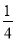 ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.