题目内容
5.某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=-x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
分析 (1)由“每月游客人数控制在200人以内”知y<200,据此列不等式求解可得;
(2)根据“总成本=每人的成本价×游客人数”可得函数解析式,据此根据一次函数性质可得;
(3)根据“总利润=每人的利润×游客人数”得出总利润关于报价的函数解析式,配方成顶点式,利用二次函数的性质可得其最值情况.
解答 解:(1)由题意得y<200时,即-x+1300<200,
解得:x>1100,
即该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)设经营这条旅游线路每月所需要的成本为z,
∴z=500(-x+1300)=-500x+650000,
∵-500<0,
∴当x=1200时,z最低,即z=50000;
(3)设经营这条旅游线路的总利润为w,
则w=(x-500)(-x+1300)=-x2+1800x-650000=-(x-900)2+160000,
当x=900时,w最大=160000.
点评 本题主要考查二次函数的应用,解题的关键是根据题意确定相等关系,并据此列出函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.某商店需要购进一批电视机和洗衣机,根据市场调查,经理决定电视机进货量不少于洗衣机的进货量的一半,电视机与洗衣机的进价和售价如下表:
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元,请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
13.下列各式计算的结果是正数的是( )
| A. | (-3)+2 | B. | (-3)×2 | C. | (-3)2 | D. | -23 |
17.如果关于x的方程x2+4x-m=0没有实数根,则m的取值范围是( )
| A. | m<-4 | B. | m>-4 | C. | m≤-4 | D. | m≥-4 |
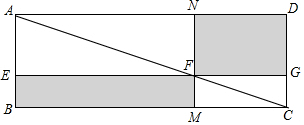 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.