Question

18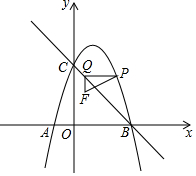．如图，在平面直角坐标系中，抛物线y=a（x-1）²+4与x轴交于点A、B两点，与y轴交于点C，且点B的坐标为（3，0），点P在这条抛物线的第一象限图象上运动．过点P作y轴的垂线与直线BC交于点Q，以PQ为边作Rt△PQF，使∠PQF=90°，点F在点Q的下方，且QF=1，设线段PQ的长度为d，点P的横坐标为m．
（1）求这条抛物线所对应的函数表达式；
（2）求d与m之间的函数关系式；
（3）当Rt△PQF的边PF被y轴平分时，求d的值；
（4）以OB为直角边作等腰直角三角形OBD，其中点D在第一象限，直接写出点F落在△OBD的边上时m的值．

Answer 1

分析 （1）把点B（3，0）代入抛物线y=a（x-1）²+4求出a即可．
（2）求出直线BC的解析式，根据P、Q两点纵坐标相同，求出点Q的横坐标即可解决问题．
（3）当Rt△PQF的边PF被y轴平分时，点P与点Q关于y轴对称，如图1中，根据P、Q两点横坐标互为相反数，列出方程即可解决问题．
（4）如图2中，分两种情形当点F在直线OD上时，当点F在直线OB上时，分别列出方程即可解决问题．

解答 解；（1）把点B（3，0）代入抛物线y=a（x-1）²+4，得4a+4=0，
∴a=-1，
∴抛物线的解析式为y=-（x-1）²+4，=-x²+2x+3．

（2）对于抛物线y=-x²+2x+3，当x=0时，y=3，
∴C（0，3），∵B（3，0），设直线BC的解析式为y=kx+b，则有$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$，
∴直线BC的解析式为y=-x+3，
∵点P坐标（m，-m²+2m+3），
∴点Q的纵坐标为-m²+2m+3，则-x+3=-m²+2m+3，
∴x=m²-2m，
∴点Q的坐标为（m²-2m，-m²+2m+3），
∵0＜m＜3，
∴d=m-（m²-2m）=-m²+3m．

（3）当Rt△PQF的边PF被y轴平分时，点P与点Q关于y轴对称，如图1中，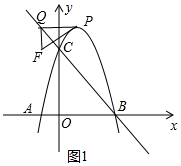

∴P、Q两点横坐标互为相反数，
∴m²-2m+m=0，解得m=1或0（舍弃），
∴m=1，d=3-1=2．

（4）如图2中，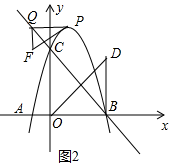

∵F（m²-2m，-m²+2m+2），
当点F在直线OD上时，m²-2m=-m²+2m+2，解得m=1+$\sqrt{2}$或1-$\sqrt{2}$（舍弃），
当点F在直线OB上时，-m²+2m+2=0，解得m=1+$\sqrt{3}$或1-$\sqrt{3}$（舍弃），
综上所述，当m=1+$\sqrt{2}$或1+$\sqrt{3}$时，点F落在△OBD的边上．

点评 本题考查二次函数综合题、待定系数法、一次函数等知识，解题的关键是灵活应用待定系数法解决问题，学会分类讨论，不能漏解，属于中考压轴题．