题目内容
如图,⊙O的圆心在x轴上,与坐标轴交于A(0,2)、B(2| 3 |
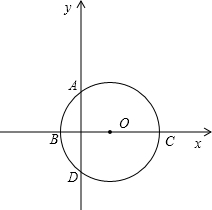 ,若抛物线y=-
,若抛物线y=-| 1 |
| 2 |
(1)求出抛物线的关系式;
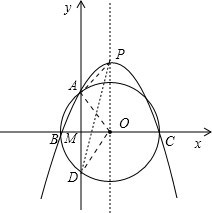
(2)抛物线的顶点P是否在圆上?
(3)若⊙O与y轴的另一交点为D,则由线段PA、线段PD及弧ABD形成的封闭图形PABD的面积为多少?
分析:(1)知A,B两点代入二次函数式求其解析式;
(2)知道二次函数式求其顶点坐标,在Rt△AMO中,由勾股定理求得OA=OB,即圆点O坐标,从而确定.
(3)连接OD,又点O在抛物线的对称轴上,得OP∥y轴,又得S△OAD=S△PAD,由线段PA、线段PD及弧ABD形成的面积,在Rt△AMO中,利用三角函数求得角AOM为60°,从而求得.
(2)知道二次函数式求其顶点坐标,在Rt△AMO中,由勾股定理求得OA=OB,即圆点O坐标,从而确定.
(3)连接OD,又点O在抛物线的对称轴上,得OP∥y轴,又得S△OAD=S△PAD,由线段PA、线段PD及弧ABD形成的面积,在Rt△AMO中,利用三角函数求得角AOM为60°,从而求得.
解答:解:(1)∵抛物线经过点A、B,
有
,
解得
,
∴y=-
x2+
x+
;
(2)由y=-
x2+
x+
得y=-
(x-1)2+
,
顶点P的坐标为(1,
),
在Rt△AMO中,OA2-OM2=AM2,AM=
,BM=1,
故有OA2-(OA-1)2=3,
∴OA=2
∴OB=2,OM=1,即点O的坐标为(1,0).
∴OP=
>2,
∴顶点P在圆外;
(3)连接OD,∵点O在抛物线的对称轴上,
∴OP∥y轴,
∴S△OAD=S△PAD,
∴由线段PA、线段PD及弧ABD形成的封闭图形PABD的面积=扇形OAD的面积.
∵在Rt△AMO中,sin∠AOM=
,
∴∠AOM=60°.
∴封闭图形PABD的面积=
•OA2=
(平方单位).
有
|

解得
|
∴y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)由y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| ||
| 3 |
4
| ||
| 3 |
顶点P的坐标为(1,
4
| ||
| 3 |
在Rt△AMO中,OA2-OM2=AM2,AM=
| 3 |
故有OA2-(OA-1)2=3,
∴OA=2
∴OB=2,OM=1,即点O的坐标为(1,0).
∴OP=
4
| ||
| 3 |
∴顶点P在圆外;
(3)连接OD,∵点O在抛物线的对称轴上,
∴OP∥y轴,
∴S△OAD=S△PAD,
∴由线段PA、线段PD及弧ABD形成的封闭图形PABD的面积=扇形OAD的面积.
∵在Rt△AMO中,sin∠AOM=
| ||
| 2 |
∴∠AOM=60°.
∴封闭图形PABD的面积=
| 120π |
| 360 |
| 4π |
| 3 |
点评:本题考查了二次函数的综合应用,考查了知道二次函数上的两点求函数式,考查了抛物线的顶点以及将其代入圆中符合即其顶点在圆上,考查了圆与直线所构成图形面积的求值.

练习册系列答案
相关题目
 ,连接BO、ED,有BO∥ED,作弦EF⊥AC于G,连接DF.
,连接BO、ED,有BO∥ED,作弦EF⊥AC于G,连接DF.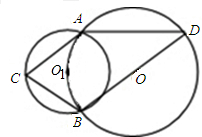 如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.
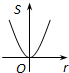
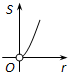
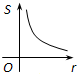
如图,⊙O1的圆心在⊙O的圆周上,⊙O和⊙O1交于A,B,AC切⊙O于A,连接CB,BD是⊙O的直径,∠D=40°,求:∠AO1B,∠ACB和∠CAD的度数.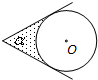 如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )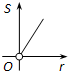
 (2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )
(2012•郧县三模)如图,⊙O的圆心在坐标原点,⊙O与x轴正半轴交于点B,延长OB至点A使AB=OB,过点A作⊙O的切线AC,切点为C,P为⊙O上一点(不在弧BC上),则cos∠BPC的值为( )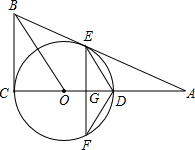 (2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
(2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.