��Ŀ����
12����ͼ��ʾ����ֱ������ϵxOy�У���O������ԭ�㣬��A��x���������ϣ�OA=12$\sqrt{3}$cm����B��y����������ϣ�OB=12cm������P�ӵ�O��ʼ��OA��2$\sqrt{3}$cm/s���ٶ����A�ƶ�������Q�ӵ�A��ʼ��AB��4cm/s���ٶ����B�ƶ�������R�ӵ�B��ʼ��BO��2cm/s���ٶ����O�ƶ������P��Q��R�ֱ��O��A��Bͬʱ�ƶ����ƶ�ʱ��Ϊts��0��t��6������1�����OAB�Ķ�����
��2��д����POR�����S�涯���ƶ�ʱ��t�ĺ�����ϵʽ������S����Сֵ����Ӧ��tֵ��
��3���Ƿ���ڡ�APQΪ���������Σ������ڣ�ֱ��д����Ӧ��tֵ���������ڣ���˵�����ɣ�
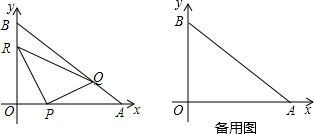
���� ��1����Rt��OAB�У���֪��OA��OB�ij������������OAB������ֵ���ɴ˿ɵõ���OAB�Ķ�����
��2����Q��QE��x����E����Rt��AQE�У�����t��ʾ��AQ�ij����������ݡ�OAB�Ķ�����ʾ��QE��AE�ij�����S��PQR=S��OAB-S��OPR-S��APQ-S��BRQ�������S��t�ĺ�����ϵʽ���������ú��������ʼ��Ա�����ȡֵ��Χ�������S����Сֵ����Ӧ��t��ֵ��
��3�����ڡ�APQ�����͵ײ�ȷ������������ۣ�
��AP=AQ���ɷֱ���t��ʾ�������߶εij���Ȼ��������ǵĵ�����ϵ�����ʱt��ֵ��
��PQ=AQ������Q��QD��x����D�����ݵ������������ߺ�һ������֪��PA=2AD���ɷֱ���t��ʾ��PA��AD�ij���Ȼ��������ǵĵ�����ϵ�з�����⣻
��AP=PQ������Q��QH��AQ��H������ͬ�ڣ�
��� �⣺��1����Rt��AOB�У�
tan��OAB=$\frac{OB}{OA}$��
���OAB=30�㣮
��2����ͼ������Q��QE��x�ڵ�E��
�ߡ�BAO=30�㣬AQ=4t��
��QE=$\frac{1}{2}$AQ=2t��
AE=AQ•cos��OAB=4t��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$t��
��OE=OA-AE=12$\sqrt{3}$-2$\sqrt{3}$t��
��Q���������12$\sqrt{3}$-2$\sqrt{3}$t��2t����
S��PQR=S��OAB-S��OPR-S��APQ-S��BRQ
=$\frac{1}{2}$��12��12$\sqrt{3}$-$\frac{1}{2}$��2$\sqrt{3}$t����12-2$\sqrt{3}$t����2t-$\frac{1}{2}$��2t����12$\sqrt{3}$-2$\sqrt{3}$��=6$\sqrt{3}$��t-3��2+18$\sqrt{3}$��0��t��6��
��t=3ʱ��S��PQR��С=18$\sqrt{3}$��
��3���������������ͼ
�ٵ�AP=AQ1=4tʱ��
��OP+AP=12$\sqrt{3}$��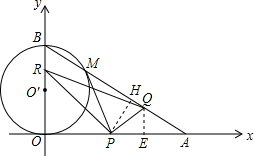
��2$\sqrt{3}$t+4t=12$\sqrt{3}$��
��t=12$\sqrt{3}$-18��
�ڵ�PQ2=AQ2=4tʱ��
��Q2����Q2E��x���ڵ�E��
��PA=2AE=2AQ2•cosA=4$\sqrt{3}$t��
��2$\sqrt{3}$t+4$\sqrt{3}$t=12$\sqrt{3}$��
��t=2��
�۵�PA=PQ3ʱ������P��PH��AB�ڵ�H��
AH=PA•cos30��=��12$\sqrt{3}$-2$\sqrt{3}$t����$\frac{\sqrt{3}}{2}$=18-3t��
AQ3=2AH=36-6t��
��36-6t=4t��
��t=3.6��
������������t=2��t=3.6��t=12$\sqrt{3}$-18ʱ����APQ�ǵ��������Σ�
���� �����������ε��ۺ��⣬��Ҫ���������ߵ��ж���ȫ�������ε��ж������ʡ����κ�����Ӧ���Լ����������ε��ж������ʵ�֪ʶ����ע����ǣ�3�����ڲ�ȷ���������������͵�����£�Ҫ��ֿ��ǵ����ֿ��ܵ����������©��

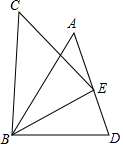 ��ͼ����֪����ABD�ա�CBE�����н��۲���ȷ���ǣ�������
��ͼ����֪����ABD�ա�CBE�����н��۲���ȷ���ǣ�������| A�� | ��CBE=��ABD | B�� | BE=BD | C�� | ��CEB=��BDE | D�� | AE=ED |
 ��ͼ����ԲԲ����ͬ����Բ����AB��СԲ���У�AB=8����ͼ����Ӱ���ֵ�����ǣ�������
��ͼ����ԲԲ����ͬ����Բ����AB��СԲ���У�AB=8����ͼ����Ӱ���ֵ�����ǣ�������| A�� | 8�� | B�� | 4�� | C�� | 64�� | D�� | 16�� |
| A�� | 6a-5a=1 | B�� | a3•a3=a9 | C�� | a6��a3=a2 | D�� | ��a2��3=a6 |
 ��ͼ���ڡ�ABC�У�AC=BC����ACB=90�㣬AEƽ�֡�BAC��BC��E��BD��AE��D��DM��AC��AC���ӳ�����M������CD������������ۣ��١�CAD=��CBD����S��DBC=S��AEC���ۡ�ADC=45�㣻��AC+CE=AB����CE=2MC��������ȷ�Ľ����У�������
��ͼ���ڡ�ABC�У�AC=BC����ACB=90�㣬AEƽ�֡�BAC��BC��E��BD��AE��D��DM��AC��AC���ӳ�����M������CD������������ۣ��١�CAD=��CBD����S��DBC=S��AEC���ۡ�ADC=45�㣻��AC+CE=AB����CE=2MC��������ȷ�Ľ����У�������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
| A�� | 2��$\frac{1}{2}$ | B�� | -��+3����+��-3�� | C�� | -1��-��-1�� | D�� | 2��|-2| |
| A�� | 3x2-6xy+2=0 | B�� | x2-5=-2x | C�� | x2+3x-1=x2 | D�� | x2+$\frac{1}{x}$=0 |
| A�� | -3 | B�� | 3 | C�� | 23 | D�� | -23 |