题目内容
4.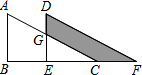 如图,将Rt△ABC平移至△DEF所示位置得到四边形DGCF的面积为12,且∠B=90°,AB=5,DG=2,则CF=3.
如图,将Rt△ABC平移至△DEF所示位置得到四边形DGCF的面积为12,且∠B=90°,AB=5,DG=2,则CF=3.
分析 根据平移的性质可知:AB=DE,设BE=CF=x;由此可求出EH和CF的长.由于CH∥DF,可得出△ECH∽△EFD,根据相似三角形的对应边成比例,可求出EC的长.已知了EH、EC,DE、EF的长,即可求出△ECH和△EFD的面积,进而可根据阴影部分的面积求得x的值即可.
解答 解:根据题意得,DE=AB=5;
设BE=CF=x,
∵CH∥DF.
∴EG=5-2=3;
EG:GD=EC:CF,
即 3:2=EC:x,
∴EC=$\frac{3}{2}$x,
∴EF=EC+CF=$\frac{5}{2}$x,
∴S△EFD=$\frac{1}{2}$×$\frac{5}{2}$x×5=$\frac{25}{4}$x;
S△ECG=$\frac{1}{2}$×3×$\frac{3}{2}$x=$\frac{9}{4}$x.
∴S阴影部分=$\frac{25}{4}$x-$\frac{9}{4}$x=12.
解得:x=3.
故答案为3.
点评 此题考查平移的性质、相似三角形的判定与性质及有关图形的面积计算,有一定的综合性.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
9.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a4÷a4=a | C. | a2•a3=a6 | D. | (-a2)3=-a6 |
16.下列由题意列出的不等关系中,错误的是( )
| A. | “a不是负数”表示为a>0 | |
| B. | “m与4的差是非负数”表示为m-4≥0 | |
| C. | “x不大于3”表示为x≤3 | |
| D. | “代数式x2+3大于3x-7”表示为x2+3>3x-7 |
13.△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列命题是假命题的是( )
| A. | 若∠C-∠B=∠A,则△ABC是直角三角形 | |
| B. | 若c2=b2-a2,则△ABC是直角三角形且∠C是直角 | |
| C. | 若(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| D. | 若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形且∠A为直角 |
14.计算(a2)4÷a5÷a的结果为( )
| A. | a5 | B. | a4 | C. | a3 | D. | a2 |
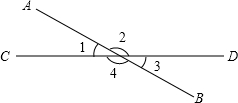 如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2和∠4.
如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2和∠4. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为4cm.
如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为4cm.