题目内容
【题目】在![]() 中,
中,![]() .
.
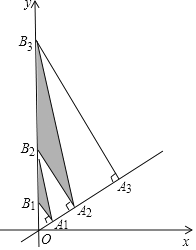
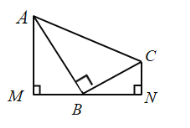
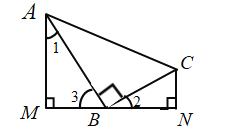
(1)如图.分别过![]() 、
、![]() 两点作经过点
两点作经过点![]() 的直线的垂线,垂足分别为
的直线的垂线,垂足分别为![]() 、
、![]() ,求证:
,求证:![]() .
.
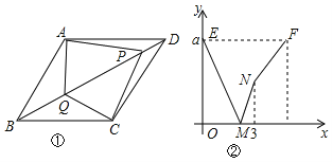
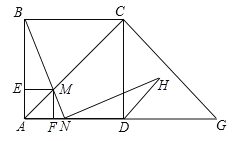
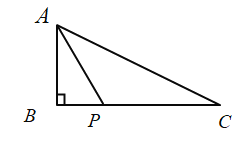
(2)如图,![]() 是边
是边![]() 上一点,
上一点,![]() ,
,![]() ,求
,求![]() 的值.
的值.
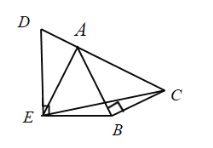
(3)如图,![]() 是边
是边![]() 延长线上一点,
延长线上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)见解析 (2)![]() (3)
(3)![]()
【解析】
(1)由题意,只要证明△AMB∽△BNC,即可得到结论成立;
(2)过![]() 点作
点作![]() 交
交![]() 于
于![]() 点,过
点,过![]() 作
作![]() 于
于![]() 点,先证明
点,先证明![]() ,得到
,得到![]() ,再证明
,再证明![]() ,即可得到结论成立;
,即可得到结论成立;
(3)作AG⊥BE于G,作CH⊥BE于点H,先判断出![]() ,再同(2)的方法,即可得出结论.
,再同(2)的方法,即可得出结论.
证明:(1):![]() ,
,
![]() ,
,
又![]() ,
,
∴∠M=∠N=90°,∠1+∠3=90°,
∴∠1=∠2.
![]() ,
,
![]() ;
;
(2)过![]() 点作
点作![]() 交
交![]() 于
于![]() 点,过
点,过![]() 作img src="https://thumb.zyjl.cn/questionBank/Upload/2020/07/22/04/8078862f/SYS202007220422182855736715_DA/SYS202007220422182855736715_DA.007.png" width="72" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于
作img src="https://thumb.zyjl.cn/questionBank/Upload/2020/07/22/04/8078862f/SYS202007220422182855736715_DA/SYS202007220422182855736715_DA.007.png" width="72" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />于![]() 点,
点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,![]()
又![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
解得:![]() ,
,
![]() ;
;
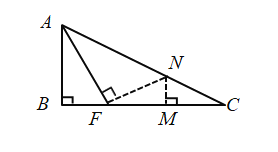
(3)如图,作AG⊥BE于G,作CH⊥BE于点H,
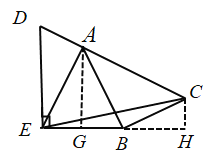
在Rt△ABC中,![]() ,
,
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
同(1)的方法得,△ABG∽△BCH
∴![]() ,
,
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∴![]() ,
,
∴n=2m,
∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,
在Rt△CEH中,tan∠BEC=![]() .
.
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案