题目内容
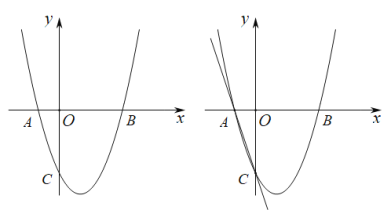
【题目】如图,抛物线![]() 的与
的与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
(1)求该抛物线的解析式及顶点的坐标;
(2)若![]() 是线段
是线段![]() 上一动点,过
上一动点,过![]() 作
作![]() 轴的平行线交抛物线于点
轴的平行线交抛物线于点![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 时,
时,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式;若
的函数关系式;若![]() 有最大值,请求出
有最大值,请求出![]() 的最大值,若没有,请说明理由;
的最大值,若没有,请说明理由;
(3)若![]() 是
是![]() 轴上一个动点,过
轴上一个动点,过![]() 作射线
作射线![]() 交抛物线于点
交抛物线于点![]() ,随着
,随着![]() 点的运动,在
点的运动,在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,使以
,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请直接写出
为顶点的四边形为平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 有最大值,最大值是
有最大值,最大值是![]() ;(3)存在,
;(3)存在,![]() 点为
点为![]() ,
,![]() ,
,![]()
【解析】
(1)根据待定系数法即可求出抛物线的解析式,把一般式转化为顶点式即得顶点坐标;
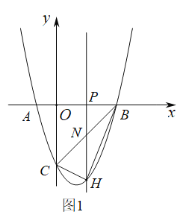
(2)如图1,先求出点B坐标,然后利用待定系数法求出直线BC的解析式,由![]() ,则点H、N的横坐标都可以用含t的代数式表示,由
,则点H、N的横坐标都可以用含t的代数式表示,由![]() 即可得到S与t的函数关系式,进一步即可根据二次函数的性质求出S的最大值;
即可得到S与t的函数关系式,进一步即可根据二次函数的性质求出S的最大值;
(3)设![]() ,分两种情况:①如图2,当
,分两种情况:①如图2,当![]() 在
在![]() 轴下方时,作
轴下方时,作![]() 轴于
轴于![]() ,由平行四边形的性质可证得
,由平行四边形的性质可证得![]() ,从而可得
,从而可得![]() ,由此可得关于x的方程,解方程即可求x的值,进而可得点P坐标;②如图3,当
,由此可得关于x的方程,解方程即可求x的值,进而可得点P坐标;②如图3,当![]() 在
在![]() 轴上方时,作
轴上方时,作![]() 轴于
轴于![]() ,同①的方法解答即可.
,同①的方法解答即可.
解(1)将![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,解得:
,解得:![]() ,
,
∴抛物线的表达式为:![]() ;
;
∴抛物线的顶点坐标为![]() ;
;
(2)由![]() ,得x=3或x=﹣1,则点
,得x=3或x=﹣1,则点![]() ,
,
如图1,连接![]() 、
、![]() 、
、![]() ,设直线
,设直线![]() 解析式为
解析式为![]() ,代入
,代入![]() ,
,![]() ,得:
,得:
![]() ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
则当![]() 时,
时,![]() 有最大值,最大值是
有最大值,最大值是![]() ;
;
(3)存在,P点坐标为![]() ,
,![]() ,
,![]() ;
;
理由如下:设![]() ,
,
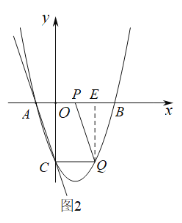
①如图2,当![]() 在
在![]() 轴下方时,作
轴下方时,作![]() 轴于
轴于![]() ,
,
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (与
(与![]() 点重合,舍去),
点重合,舍去),
∴![]() ;
;
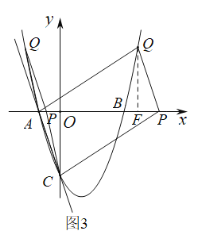
②如图3,当![]() 在
在![]() 轴上方时,作
轴上方时,作![]() 轴于
轴于![]() ,
,
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
∴![]() ,
,![]() ;
;
综上所述,![]() 点为
点为![]() ,
,![]() ,
,![]() .
.

【题目】甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
甲 |
|
|
| 10 |
|
乙 |
|
|
|
|
|
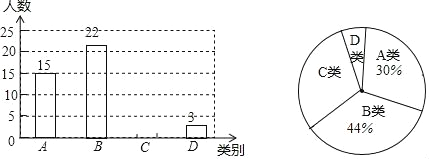
(1)乙种水稻5年的平均单位面积产量的平均数为______吨/公顷;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映甲种水稻5年的平均单位面积产量变化过程和趋势的统计图是______;
(3)王老汉家有100公顷田要种植水稻,你建议他种什么品种的水稻,并说明理由.
【题目】港珠澳大桥(英文名称:Hong Kong-Zhuhai-Macao Bridge)是中国境内一座连接香港、广东珠海和澳门的桥隧工程,位于中国广东省珠江口伶洋海域内,为珠江三角洲地区环线高速公路南环段.港珠澳大桥于![]() 年
年![]() 月
月![]() 日动工建设;于
日动工建设;于![]() 年
年![]() 月
月![]() 日实现主体工程全线贯通;于
日实现主体工程全线贯通;于![]() 年
年![]() 月
月![]() 日完成主体工程验收;同年
日完成主体工程验收;同年![]() 月
月![]() 日上午
日上午![]() 时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
时开通运营.广东某校数学“综合与实践”小组的同学把“测量港珠澳大桥某一段斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间完成该桥斜拉索实地测量,测量结果如下表
项目 | 内容 | ||
课题 | 测量港珠澳大桥某一段斜拉索顶端到桥面的距离 | ||
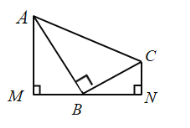
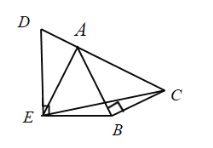
测量示意图 |
| 说明:两侧斜拉索 | |
测量数据 |
|
|
|
|
|
| |
|
| ||

(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点![]() 到
到![]() 的距离(参考数据:
的距离(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可)?