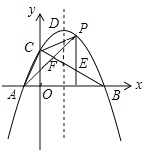ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() БпЩЯвЛЖЏЕуЃЈВЛгыЖЫЕу
БпЩЯвЛЖЏЕуЃЈВЛгыЖЫЕу![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌзїЯпЖЮ
ЃЌзїЯпЖЮ![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() НЛБп
НЛБп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
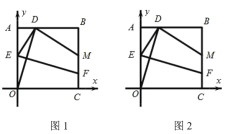
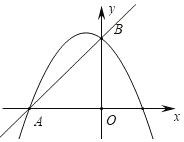
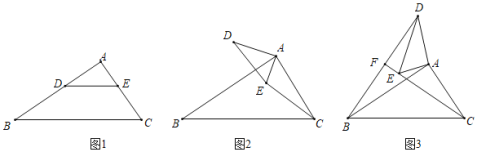
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() ЮЊЯпЖЮABЕФжаЕуЪБЃЌЧѓЯпЖЮ
ЮЊЯпЖЮABЕФжаЕуЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєе§ЗНаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌ
ЃЌ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌМЧ
ЃЌМЧ![]() ЃЌЪджЄУї
ЃЌЪджЄУї![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
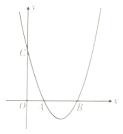
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙЙдьЙ§ЕуCЕФХзЮяЯп![]() ЭЌЪБТњзувдЯТСНИіЬѕМўЃК
ЭЌЪБТњзувдЯТСНИіЬѕМўЃК
Ђй![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌЧѓЖўДЮЯюЯЕЪ§
ЃЌЧѓЖўДЮЯюЯЕЪ§![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЖўДЮЯюЯЕЪ§
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЖўДЮЯюЯЕЪ§![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩш![]() ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬПЩЕУ
ЃЌИљОнЙДЙЩЖЈРэСаЗНГЬПЩЕУ![]() ЕФжЕЃЌДгЖјЕУDEЃЌAEЕФжЕЃЌжЄУїЁїAEDЁзЁїBDMЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУDMЕФГЄЃЛ ЃЈ2ЃЉе§ЗНаЮOABCЕФжмГЄЮЊ
ЕФжЕЃЌДгЖјЕУDEЃЌAEЕФжЕЃЌжЄУїЁїAEDЁзЁїBDMЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУDMЕФГЄЃЛ ЃЈ2ЃЉе§ЗНаЮOABCЕФжмГЄЮЊ![]() ЃЌЩш
ЃЌЩш![]() ЃЌБэЪО
ЃЌБэЪО![]() ЃЌИљОнЙДЙЩЖЈРэНЈСЂ
ЃЌИљОнЙДЙЩЖЈРэНЈСЂ![]() жЎМфЕФЙиЯЕЪНЃЌгЩЃЈ1ЃЉжаЕФЯрЫЦСаБШР§ЪНПЩБэЪОBM ЃЌDM ЃЌМЦЫуЁїBMDЕФжмГЄЮЊ
жЎМфЕФЙиЯЕЪНЃЌгЩЃЈ1ЃЉжаЕФЯрЫЦСаБШР§ЪНПЩБэЪОBM ЃЌDM ЃЌМЦЫуЁїBMDЕФжмГЄЮЊ![]() ЃЌДњШыПЩЧѓЕУmЕФжЕЃЛ ЃЈ3ЃЉЯШРћгУ
ЃЌДњШыПЩЧѓЕУmЕФжЕЃЛ ЃЈ3ЃЉЯШРћгУ![]() гывбжЊЬѕМўЕУЕН
гывбжЊЬѕМўЕУЕН![]() гы
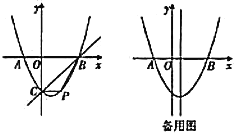
гы![]() ЕФЙиЯЕЃЌаДГіХзЮяЯпЕФНтЮіЪНЃЌПЩЕУЖдГЦжсЃЌНЋЃЈ2ЃЉжаЕФmДњШыЃКЕУЕН3ЁмxЁм7ЪБЃЌyгазюДѓжЕЃЌАДПЊПкЗНЯђЗжЧщПіЬжТлПЩЕУНсТлЃЎ
ЕФЙиЯЕЃЌаДГіХзЮяЯпЕФНтЮіЪНЃЌПЩЕУЖдГЦжсЃЌНЋЃЈ2ЃЉжаЕФmДњШыЃКЕУЕН3ЁмxЁм7ЪБЃЌyгазюДѓжЕЃЌАДПЊПкЗНЯђЗжЧщПіЬжТлПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЩш![]() ЃЌвРЬтвтгаЃК
ЃЌвРЬтвтгаЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁпEDЁЭDMЃЌ ЁрЁЯEDM=ЁЯADE+ЁЯBDM=90ЁуЃЌ
ЁпЁЯADE+ЁЯAED=90ЁуЃЌ ЁрЁЯAED=ЁЯEDMЃЌ
ЁпЁЯDAE=ЁЯMBD=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМДЯпЖЮ
ЃЌМДЯпЖЮ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЎ
ЃЎ
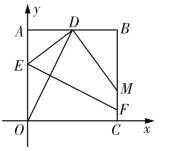
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌдђга
ЃЌдђга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌећРэЕУЃК
ЃЌећРэЕУЃК![]() ЃЎ
ЃЎ
гЩ![]() ПЩЕУЃК
ПЩЕУЃК![]() ЃЌ
ЃЌ
ДгЖјгаЃК![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌНЋ
ЃЌНЋ![]() ДњШыЃЌПЩЕУ
ДњШыЃЌПЩЕУ![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЛЁр
ЃЛЁр![]() ЮЊЖЈжЕЃЎ
ЮЊЖЈжЕЃЎ
ЃЈ3ЃЉЁпХзЮяЯп![]() ОЙ§
ОЙ§![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌЦфЖдГЦжсЮЊ
ЃЌЦфЖдГЦжсЮЊ![]() ЃЎ
ЃЎ
гЩ![]() ПЩжЊЕБ
ПЩжЊЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ
гкЪЧгаЃКЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБга
ЪБга![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБга
ЪБга![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌЖўДЮЯюЯЕЪ§![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ