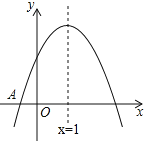Question

【题目】如图，在平面直角坐标系中，抛物线与轴正半轴交于两点（点在点左侧），与轴交于点．

（1）利用直尺和圆规，作出抛物线的对称轴（尺规作图，保留作图痕迹，不写作法）；

（2）若是等腰直角三角形，且其腰长为3，求的值；

（3）在（2）的条件下，点为抛物线对称轴上的一点，则的最小值为________．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）利用基本作图，作AB的垂直平分线即可；
（2）根据等腰直角三角形的性质得到OB=OC=3，则C（0，3），B（3，0），然后利用待定系数法求抛物线解析式；
（3）连接BC交直线l于P，如图，根据两点之间线段最短可判断此时PC+PA的值最小，然后根据等腰直角三角形的性质计算出BC即可．

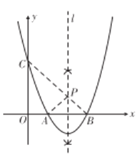
解：（1）如图，直线为所作；

（2）是等腰直角三角形，且其腰长为3，

即，

把分别代入中

得：

解得．

（3）连接交直线于点，如图，则．

此时的值最小，

而

的最小值为．

故答案为．