题目内容
18.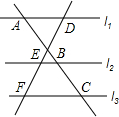 如图所示,已知:l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{m}{n}$,试说明:$\frac{DE}{DF}$=$\frac{m}{m+n}$.
如图所示,已知:l1∥l2∥l3,$\frac{AB}{BC}$=$\frac{m}{n}$,试说明:$\frac{DE}{DF}$=$\frac{m}{m+n}$.
分析 根据平行线分线段成比例定理得到$\frac{AB}{BC}$=$\frac{DE}{EF}$=$\frac{m}{n}$,然后根据比例的性质即可得到结论.
解答 证明:∵:l1∥l2∥l3,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$=$\frac{m}{n}$,
∴$\frac{DE}{DE+EF}$=$\frac{m}{m+n}$,
即$\frac{DE}{DF}$=$\frac{m}{m+n}$.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
相关题目
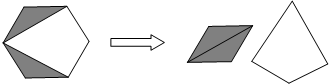
8.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为 ( )

| A. | 5a | B. | 4a | C. | 3a | D. | 2a |
9.我国第六次全国人口普查数据显示,居住在城镇的人口总数大约为6 6600 0000人,用科学记数法表示为( )
| A. | 66.6×107 | B. | 6.66×108 | C. | 6.66×107 | D. | 0.666×109 |
8.下列说法正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 在同一平面内,若a丄b,b丄c,则a∥c | |
| C. | 内错角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
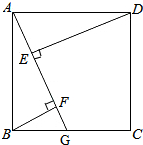 如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.


