题目内容
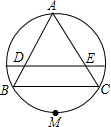 如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,若BC=5,则折痕在△ABC内的部分DE的长为( )
如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,若BC=5,则折痕在△ABC内的部分DE的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:AM与DE交于点F,则F是△ABC的内心,同时又是重心,依据重心的性质即可得出AF与AS的比值;再根据相似三角形的性质,对应边的比相等,即可求解.
解答: 解:如图,连接AM,与DE、BC分别交于点F、点S,
解:如图,连接AM,与DE、BC分别交于点F、点S,
则点F是圆心,又是三角形的内心;
∵点S是BC的中点,点F是DE的中点,
则有DE∥BC,
∴AF:AS=DE:BC=2:3,
∴DE=
.
故选C.
 解:如图,连接AM,与DE、BC分别交于点F、点S,
解:如图,连接AM,与DE、BC分别交于点F、点S,则点F是圆心,又是三角形的内心;
∵点S是BC的中点,点F是DE的中点,
则有DE∥BC,
∴AF:AS=DE:BC=2:3,
∴DE=
| 10 |
| 3 |
故选C.
点评:本题利用了圆的内接正三角形的内心到每个顶点的距离是等边三角形高的
的性质,进行求解.
| 2 |
| 3 |

练习册系列答案
相关题目
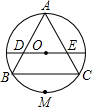 如图,把正△ABC的外接圆对折,使点A与劣弧
如图,把正△ABC的外接圆对折,使点A与劣弧 |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
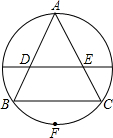 如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则折痕在△ABC内的部分DE长为
如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则折痕在△ABC内的部分DE长为 如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则正△ABC的外接圆半径为
如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则正△ABC的外接圆半径为