题目内容
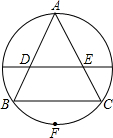 如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则折痕在△ABC内的部分DE长为
如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则折痕在△ABC内的部分DE长为分析:根据△ADE∽△ABC,相似三角形对应边的比相等,即可求解.
解答: 解:连接AF,交BC于点G,AF与DE交于圆心O,如图所示,
解:连接AF,交BC于点G,AF与DE交于圆心O,如图所示,
可得AF⊥BC,AF⊥DE,
∴DE∥BC,∠OGB=90°,
设OG=b,
由题意可得∠OBG=
∠ABC=30°,
∴OA=OB=2b,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=OA:AG,
∴DE=
.
故答案为:
.
 解:连接AF,交BC于点G,AF与DE交于圆心O,如图所示,
解:连接AF,交BC于点G,AF与DE交于圆心O,如图所示,可得AF⊥BC,AF⊥DE,
∴DE∥BC,∠OGB=90°,
设OG=b,
由题意可得∠OBG=
| 1 |
| 2 |
∴OA=OB=2b,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=OA:AG,
∴DE=
| 10 |
| 3 |
故答案为:
| 10 |
| 3 |
点评:本题用到的知识点为:相似三角形的高的比等于相似比.

练习册系列答案
相关题目
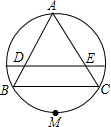 如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,若BC=5,则折痕在△ABC内的部分DE的长为( )
如图,把正△ABC的外接圆对折,使点A与劣弧的中点M重合,若BC=5,则折痕在△ABC内的部分DE的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
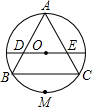 如图,把正△ABC的外接圆对折,使点A与劣弧
如图,把正△ABC的外接圆对折,使点A与劣弧 |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则正△ABC的外接圆半径为
如图,把正△ABC的外接圆对折,使点A落在弧BC的中点F上,若BC=5,则正△ABC的外接圆半径为