题目内容
 如图,AB⊥AC,∠DAB=∠C,则∠C+∠CAD=
如图,AB⊥AC,∠DAB=∠C,则∠C+∠CAD=考点:余角和补角
专题:
分析:根据垂直定义得出∠CAB=∠DAB+∠CAD=90°,把∠DAB=∠C代入,即可求出答案.
解答:解:∵AB⊥AC,
∴∠CAB=∠DAB+∠CAD=90°,
∵∠DAB=∠C,
∴∠C+∠CAD=90°,
故答案为:90°.
∴∠CAB=∠DAB+∠CAD=90°,
∵∠DAB=∠C,
∴∠C+∠CAD=90°,
故答案为:90°.
点评:本题考查了垂直定义,余角的应用,解此题的关键是求出∠DAB+∠CAD=90°,注意:已知∠A,则∠A的余角=90°-∠A.

练习册系列答案
相关题目
从直观上看,下列线段中最长的是( )
A、 |
B、 |
C、 |
D、 |
下面说法错误的是( )
| A、两点确定一条直线 |
| B、同角的补角相等 |
| C、等角的余角相等 |
| D、射线AB也可以写作射线BA |
正方形具有而菱形不一定具有的性质是( )
| A、对角线互相垂直 |
| B、对角线相等 |
| C、对角线互相平分 |
| D、对角相等 |
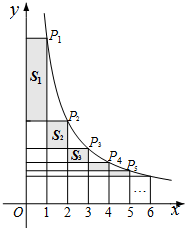 在函数
在函数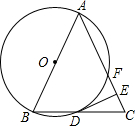 如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AB于点F,过D点作DE⊥AC于E点,试确定直线DE与⊙O的位置关系,并说明理由.
如图,以等腰三角形ABC的腰AB为直径的⊙O交底边BC于点D,交腰AB于点F,过D点作DE⊥AC于E点,试确定直线DE与⊙O的位置关系,并说明理由.