题目内容
6. 如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)求证:AB=AC;
(2)若PC=2$\sqrt{5}$,求⊙O的半径及线段PB的长.
分析 (1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC推出52-r2=(2$\sqrt{5}$)2-(5-r)2,求出r,证△DPB∽△CPA,得出$\frac{CP}{PD}$=$\frac{AP}{BP}$,代入求出即可.
解答 证明:(1)如图1,连接OB.
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)如图2,延长AP交⊙O于D,连接BD,
设圆半径为r,则OP=OB=r,PA=5-r,
则AB2=OA2-OB2=52-r2,
AC2=PC2-PA2=(2$\sqrt{5}$)2-(5-r)2,
∴52-r2=(2$\sqrt{5}$)2-(5-r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴$\frac{CP}{PD}$=$\frac{AP}{BP}$,
∴$\frac{2\sqrt{5}}{3+3}$=$\frac{5-3}{BP}$,
解得:PB=$\frac{6\sqrt{5}}{5}$.
∴⊙O的半径为3,线段PB的长为$\frac{6\sqrt{5}}{5}$.
点评 本题考查了等腰三角形的性质和判定,相似三角形的性质和判定,切线的性质,勾股定理,直线与圆的位置关系等知识点的应用,主要培养学生运用性质进行推理和计算的能力.本题综合性比较强,有一定的难度.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | 掷一枚硬币,正面一定朝上 | |
| B. | 某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖 | |
| C. | 旅客上飞机前的安检应采用抽样调查 | |
| D. | 方差越大,数据的波动越大 |

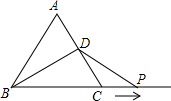 如图,等边三角形ABC的边长为10厘米.点D是边AC的中点.动点P从点C出发,沿BC的延长线以2厘米/秒的速度作匀速运动,设点P的运动时间为t(秒).若△BDP是等腰三角形,则为t=2.5.
如图,等边三角形ABC的边长为10厘米.点D是边AC的中点.动点P从点C出发,沿BC的延长线以2厘米/秒的速度作匀速运动,设点P的运动时间为t(秒).若△BDP是等腰三角形,则为t=2.5.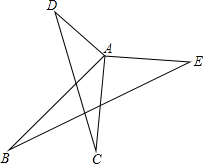 如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.
如图,已知AD⊥AB,AC⊥AE,且AD=AB,AC=AE,请判断BE和CD的关系并证明.