题目内容
(1)已知如图①、②,正方形ABCD,(1)在图①的正方形ABCD内,找一点P使∠BPC=90°,画出这个点;
(2)在图②正方形ABCD内,找出所有点P使∠BPC=60°,用尺规作图作出图形(作图保留痕迹不用写作法,写出结论)
(3)已知正方形纸片的边长为4,从这样的纸片中剪出两个最大的且全等的三角形纸片△BCP和△ADP1,使∠AP1D=∠BPC=60°,在图③画出这两个三角形,并求出剪出的一个三角形纸片的面积.

(2)在图②正方形ABCD内,找出所有点P使∠BPC=60°,用尺规作图作出图形(作图保留痕迹不用写作法,写出结论)
(3)已知正方形纸片的边长为4,从这样的纸片中剪出两个最大的且全等的三角形纸片△BCP和△ADP1,使∠AP1D=∠BPC=60°,在图③画出这两个三角形,并求出剪出的一个三角形纸片的面积.

分析:(1)如图1,以BC为直径作上半圆(不含点B、C),根据直径所对的圆周角为直角得到该半圆上的任意一点即可;
(2)①以BC为边在正方形内作等边△BCE;②作△BCE的外接圆⊙O,分别与AB、DC交于点M、N,由于在⊙O中,弧
的圆周角均为60°,所以
上的所有点均为所求的点P;
(3)同(2)作出
,交AB于M,交CD于N,连接AC,BD,交于H点,
与AC交于P点,与AC分别交于P,P1,确定出两个最大的且全等的三角形纸片△BCP和△ADP1,且∠AP1D=∠BPC=60°,如图3所示,取BC的中点G,连接GH,OP,过O作OQ⊥CP,利用垂径定理得到Q为CP的中点,由(2)得到OG为边长为4的等边三角形高的
,HG为正方形边长的一半,由HG-OG求出OH的长,由三角形OGH为等腰直角三角形,求出OQ的长,在直角三角形OPQ中,利用勾股定理求出PQ的长,确定出PC的长,根据正方形的对角线互相垂直得到BH垂直与PC,利用三角形的面积公式即可求出三角形BPC的面积.
(2)①以BC为边在正方形内作等边△BCE;②作△BCE的外接圆⊙O,分别与AB、DC交于点M、N,由于在⊙O中,弧
 |
| BC |
 |
| MN |
(3)同(2)作出
 |
| MN |
 |
| MN |
| 1 |
| 3 |
解答: 解:(1)如图1,以BC为直径作上半圆(不含点B、C),
解:(1)如图1,以BC为直径作上半圆(不含点B、C),
则该半圆上的任意一点即可;
(2)如图2,以BC为一边作等边△EBC,作△EBC的外接圆⊙O分别与AB,DC交于点 M、N,
即为点P的集合;
(3)同(2)作出
,交AB于M,交CD于N,连接AC,BD,交于H点,
与AC交于P点,
同理确定出P1,可得出∠BPC=∠AP1D=60°,
得到两个最大的且全等的三角形纸片△BCP和△ADP1,
∵四边形ABCD为正方形,
∴AC⊥BD,∠HBC=∠HCB=45°,
∴△BHC为等腰直角三角形,
取BC的中点G,连接GH,OP,过O作OQ⊥CP,
∴Q为PC的中点,
∵BC=4,HG为斜边BC上的中线,
∴HG=2,
由(2)得到OG=
×2
=
,
∴OH=HG-OG=2-
,
∵△OHQ为等腰直角三角形,
∴OQ=
OH=
(2-
),
在Rt△OPQ中,OP=
×2
=
,
根据勾股定理得:PQ=
=
,
∴CP=2PQ=
,
则S△BPC=
CP•BH=
.
 解:(1)如图1,以BC为直径作上半圆(不含点B、C),
解:(1)如图1,以BC为直径作上半圆(不含点B、C),则该半圆上的任意一点即可;
(2)如图2,以BC为一边作等边△EBC,作△EBC的外接圆⊙O分别与AB,DC交于点 M、N,
 |
| MN |
(3)同(2)作出
 |
| MN |
 |
| MN |
同理确定出P1,可得出∠BPC=∠AP1D=60°,
得到两个最大的且全等的三角形纸片△BCP和△ADP1,
∵四边形ABCD为正方形,
∴AC⊥BD,∠HBC=∠HCB=45°,
∴△BHC为等腰直角三角形,
取BC的中点G,连接GH,OP,过O作OQ⊥CP,
∴Q为PC的中点,
∵BC=4,HG为斜边BC上的中线,
∴HG=2,
由(2)得到OG=
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
∴OH=HG-OG=2-
2
| ||
| 3 |
∵△OHQ为等腰直角三角形,
∴OQ=
| ||
| 2 |
| ||
| 2 |
2
| ||
| 3 |
在Rt△OPQ中,OP=
| 2 |
| 3 |
| 3 |
4
| ||
| 3 |
根据勾股定理得:PQ=
| OP2-OQ2 |
2
| ||||
| 3 |
∴CP=2PQ=
4
| ||||
| 3 |
则S△BPC=
| 1 |
| 2 |
4
| ||||||
| 3 |
点评:此题考查了圆的综合题,涉及的知识有:圆周角定理,正方形的性质,垂径定理,勾股定理,以及尺规作图,综合利用正方形的性质和同圆中同弧所对的圆周角相等得知识点是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )


| A、AB2=AC2+BC2 | ||||||
| B、BC2=AC•BA | ||||||
C、
| ||||||
D、
|
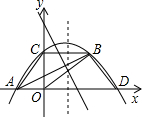 过△ABC的三个顶点,
过△ABC的三个顶点,
 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. 已知如图,菱形ABCD中,∠ADC=120°,BD=2
已知如图,菱形ABCD中,∠ADC=120°,BD=2