Question

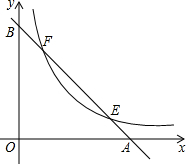如图，已知直线y=-x+2分别与x轴，y轴交于A，B两点，与双曲线y=

k

x

交于E，F两点，若AB=2EF，则k的值是（　　）

• A、-1
• B、1
• C、

  1

  2

• D、

  3

  4

Answer 1

考点：反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,等腰直角三角形

专题：

分析：作FH⊥x轴，EC⊥y轴，FH与EC交于D，先利用一次函数图象上点的坐标特征得到A（2，0），B（0，2），易得△AOB为等腰直角三角形，则AB=

2

OA=2

2

，所以EF=

1

2

AB=

2

，且△DEF为等腰直角三角形，则FD=DE=

2

2

EF=1；设F点坐标为（t，-t+2），则E点坐标为（t+1，-t+1），根据反比例函数图象上点的坐标特征得到t（-t+2）=（t+1）•（-t+1），解得t=

1

2

，这样可确定E点坐标为（

3

2

，

1

2

），然后根据反比例函数图象上点的坐标特征得到k=

3

2

×

1

2

．

解答：解：作FH⊥x轴，EC⊥y轴，FH与EC交于D，如图，
A点坐标为（2，0），B点坐标为（0，2），OA=OB，
∴△AOB为等腰直角三角形，
∴AB=

2

OA=2

2

，
∴EF=

1

2

AB=

2

，
∴△DEF为等腰直角三角形，
∴FD=DE=

2

2

EF=1，
设F点坐标为（t，-t+2），则E点坐标为（t+1，-t+1），
∴t（-t+2）=（t+1）•（-t+1），解得t=

1

2

，
∴E点坐标为（

3

2

，

1

2

），
∴k=

3

2

×

1

2

=

3

4

．
故选：D．

点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=

k

x

（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．