Question

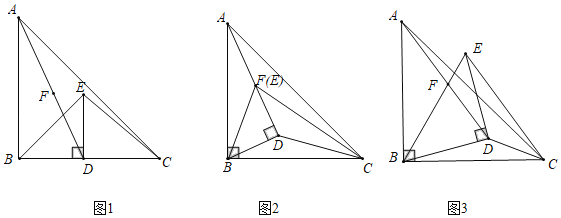
【题目】如图，在△ABC中，∠ABC＝90°，AB＝BC，点D为BC边上任意一点(与B、C不重合)，以BD为直角边构造等腰直角三角形BDE，F为AD的中点.

(1)将△BDE绕点B旋转，当点E与F重合时，求证：∠BAE+∠BCD＝45°.

(2)将△BDE绕点B旋转，当点F在BE上且AB＝AD时，求证：2CD＝BE.

Answer 1

【答案】(1)证明见解析；(2)证明见解析.

【解析】

(1)如图2中，利用等腰直角三角形的性质及旋转的性质，证明△ABF≌△BCD(SAS)即可解决问题.

(2)如图3中，作AN⊥BM于N交BE于G，CM⊥BD于M.只要证明△CDM是等腰直角三角形，BN＝DN＝DM，即可解决问题.

（1）证明：如图2中，

∵△BDE是等腰直角三角形，△BDE绕点B旋转，当点E与F重合，

∴△BFD是得把直角三角形，

∴∠DBF＝∠BFD＝45°，BD＝DF，

∵F为AD的中点，

∴AF＝DF，

∴BD＝AF，

∵∠ABC＝90°，

∴∠ABF+∠DBC＝∠ABF+∠BAF＝45°，

∴∠BAF＝∠DBC，

∵AB＝BC，

∴△ABF≌△BCD(SAS)，

∴ABF＝∠BCD，

∴∠BAE+∠BCD＝45°；

（2）证明：如图3中，作AN⊥BM于N交BE于G，CM⊥BD于M.

由(1)可知△CBM≌△BAN，

∴BN＝CM，AN＝BM，

∵AB＝AD，AN⊥BD，

∴BN＝DN，∵ED⊥BD，

∴AN∥DE，

∴∠GAF＝∠FDE，BG＝GE，

∴DE＝2GN，

在△AGF和△DEF中，，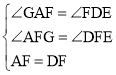

∴△AGF≌△DEF(AAS)，

∴AG＝DE＝BD，

∴AN＝3BN，BM＝3CM，

∵BN＝DN，

∴DM＝CM，

∴△CDM是等腰直角三角形，

∴CD＝CM，

∵CM＝BN＝BD，

∴CD＝BD，

∵BE＝BD，

∴BE＝2CD.