题目内容
14. 如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:△ABC是等边三角形;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
分析 (1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得.
解答 证明:(1)△ABC是等边三角形.
证明如下:在⊙O中,
∵∠BAC与∠CPB是$\widehat{BC}$对的圆周角,∠ABC与∠APC是$\widehat{AC}$所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:△ABC是等边三角形;
(2)在PC上截取PD=AP,如图1,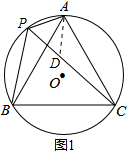
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
$\left\{\begin{array}{l}{∠APB=∠ADC}\\{∠ABP=∠ACD}\\{AP=AD}\end{array}\right.$,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
点评 本题考查了圆周角定理、等边三角形的判定、三角形的全等的判定与性质,正确作出辅助线,证明△APB≌△ADC是关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
4.我国南海海域面积约为3500000km2,用科学记数法表示数3500000为( )
| A. | 0.35×107 | B. | 3.5×106 | C. | 3.5×105 | D. | 35×105 |
2.下列4个数中:(-1)2016,|-2|,π,-32,其中正数的个数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.若a=b,则下列式子错误的是( )
| A. | $\frac{1}{3}$a=$\frac{1}{2}$b | B. | a-2=b-2 | C. | -$\frac{3}{4}a=-\frac{3}{4}b$ | D. | 5a-1=5b-1 |
 如图,已知?ABCD中,∠ABC的平分线交AD于E,cos∠AEB=$\frac{2}{3}$,求∠C的度数(精确到1′).
如图,已知?ABCD中,∠ABC的平分线交AD于E,cos∠AEB=$\frac{2}{3}$,求∠C的度数(精确到1′).