题目内容
3.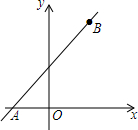 如图,在平面直角坐标系内,若一次函数y=kx+b的图象与x轴交于点A(-1,0),且经过点B(4,4),O为坐标原点,则cos∠BAO的值是$\frac{5\sqrt{41}}{41}$.
如图,在平面直角坐标系内,若一次函数y=kx+b的图象与x轴交于点A(-1,0),且经过点B(4,4),O为坐标原点,则cos∠BAO的值是$\frac{5\sqrt{41}}{41}$.
分析 过点B作BC⊥x轴于C,则在Rt△ABC中,AC=5,BC=4,所以由勾股定理求得AB的长度,由此可得cos∠BAC=$\frac{AC}{AB}$.
解答 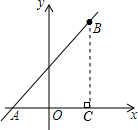 解:过点B作BC⊥x轴于C,则在Rt△ABC中,AC=5,BC=4,
解:过点B作BC⊥x轴于C,则在Rt△ABC中,AC=5,BC=4,
所以AB=$\sqrt{{5}^{2}+{4}^{2}}$=$\sqrt{41}$,
由此可得cos∠BAO=cos∠BAC=$\frac{AC}{AB}$=$\frac{5}{\sqrt{41}}$=$\frac{5\sqrt{41}}{41}$.
故答案是:$\frac{5\sqrt{41}}{41}$.
点评 本题考查了一次函数图象上点的坐标特征和锐角三角函数的定义.解答本题要注意将所给条件放在直角三角形中进行分析解答.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
11.关于x的一元二次方程x2+x+a-1=0的一个根是0,则a值为( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | $\frac{1}{2}$ |
8.关于x的一元二次方程x2+3x-2=0两根之积等于( )
| A. | -2 | B. | 3 | C. | -3 | D. | 2 |
 如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.
如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.