题目内容
(1)如图①,点A、B、C都在圆O上,若∠C=34°,则∠AOB的度数是 °
(2)如图②,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长等于 .

(2)如图②,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B,若OB=5,则BC的长等于

考点:圆周角定理,含30度角的直角三角形,勾股定理
专题:
分析:(1)直接运用圆周角定理即可解决问题.
(2)如图,作辅助线,运用直角三角形的边角关系求出AC、BC的长度,即可解决问题.
(2)如图,作辅助线,运用直角三角形的边角关系求出AC、BC的长度,即可解决问题.
解答: 解:(1)如图1,∵∠C=34°,
解:(1)如图1,∵∠C=34°,
∴∠AOB=2×34°=68°.
(2)如图2,连接CD;
∵AD为⊙O的直径,
∴∠C=90°;
∵∠CAD=30°,OB⊥AD,且OB=5,
∴cos30°=
,tan30°=
,AB=2OB=10;
∴AO=5
,AD=10
,AC=15,
∴BC=15-10=5.
 解:(1)如图1,∵∠C=34°,
解:(1)如图1,∵∠C=34°,∴∠AOB=2×34°=68°.
(2)如图2,连接CD;
∵AD为⊙O的直径,
∴∠C=90°;
∵∠CAD=30°,OB⊥AD,且OB=5,
∴cos30°=
| AC |
| AD |
| OB |
| AO |
∴AO=5
| 3 |
| 3 |
∴BC=15-10=5.
点评:该题主要考查了圆周角定理、含30°角的直角三角形的性质及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
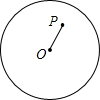 如图,P是半径为4cm的圆内一点,OP=2cm,过点P的弦与圆弧组成弓形,当过点P的弦垂直于OP时,弦与其所对的劣弧组成的弓形面积最小,那么最小弓形面积是多少?
如图,P是半径为4cm的圆内一点,OP=2cm,过点P的弦与圆弧组成弓形,当过点P的弦垂直于OP时,弦与其所对的劣弧组成的弓形面积最小,那么最小弓形面积是多少?