题目内容
已知,在同一平面直角坐标系中,正比例函数y=-2x与二次函数y=-x2+2x+c的图象交于点A(-1,m).
(1)求m,c的值;
(2)求二次函数图象的对称轴和顶点坐标.
(1)求m,c的值;
(2)求二次函数图象的对称轴和顶点坐标.
考点:二次函数的性质
专题:
分析:(1)将点A的坐标(-1,m)代入正比例函数的解析式求出m的值,再将求出的点A的坐标代入二次函数的解析式就可以求出c的值;
(2)将求出的二次函数的解析式的一般式化为顶点式就直接求出抛物线的对称轴和顶点坐标.
(2)将求出的二次函数的解析式的一般式化为顶点式就直接求出抛物线的对称轴和顶点坐标.
解答:解:(1)∵点A(-1,m)在函数y=-2x的图象上,
∴m=-2×(-1)=2,
∴点A坐标为(-1,2),
∵点A在二次函数图象上,
∴-1-2+c=2,
解得c=5;
(2)∵二次函数的解析式为y=-x2+2x+5,
∴y=-x2+2x+5=-(x-1)2+6,
∴对称轴为直线x=1,顶点坐标为(1,6).
∴m=-2×(-1)=2,
∴点A坐标为(-1,2),
∵点A在二次函数图象上,
∴-1-2+c=2,
解得c=5;
(2)∵二次函数的解析式为y=-x2+2x+5,
∴y=-x2+2x+5=-(x-1)2+6,
∴对称轴为直线x=1,顶点坐标为(1,6).
点评:本题是一道二次函数和正比例函数的综合试题,考查了利用函数的解析式求点的坐标的值以及二次函数的图象性质,运用了正比例函数和二次函数的有关知识.

练习册系列答案
相关题目
下列说法正确的是( )
| A、任意两个等腰三角形都相似 |
| B、任意两个菱形都相似 |
| C、任意两个正五边形都相似 |
| D、对应角相等的两个多边形相似 |
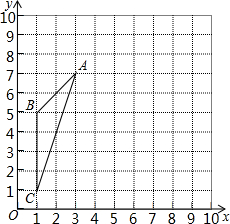 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,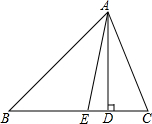 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.