Question

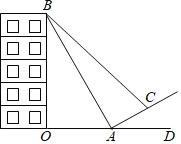
【题目】某校数学课外实践小组一次活动中，测量一座楼房的高度．如图，在山坡坡脚A处测得这座楼房的楼顶B点的仰角为60°，沿山坡往上走到C处再测得B点的仰角为45°，已知山坡的坡比i＝1：，OA＝200m，且O、A、D在同一条直线上．

(1)求楼房OB的高度；

(2)求山坡上AC的距离(结果保留根号)

Answer 1

【答案】(1)楼房OB的高度为200m；(2)山坡上AC的距离为400(2﹣)m．

【解析】

（1）根据正切的定义计算，求出OB；

（2）作CE⊥OB于E，CF⊥OD于F，设CF=xm，根据坡度的定义用x表示出AF、AC，根据等腰直角三角形的性质列方程，解方程得到答案．

解：(1)在Rt△AOB中，tan∠BAO＝，

则OB＝OAtan∠BAO＝200，

答：楼房OB的高度为200m；

(2)作CE⊥OB于E，CF⊥OD于F，

则四边形EOFC为矩形，

∴CE＝OF，CF＝OE，

设CF＝xm，

∵AC坡的坡比i＝1：，

∴AF＝x，AC＝2x，

在Rt△BEC中，∠BCE＝45°，

∴BE＝CE，即OB﹣OE＝OA+AF，

∴200﹣x＝200+x，

解得，x＝200(2﹣)

∴AC＝2x＝400(2﹣)，

答：山坡上AC的距离为400(2﹣)m．