题目内容
已知△ABC与△DEF相似且对应中线的比为2：3，则△ABC与△DEF的周长比为
2：3 ．
考点： 相似三角形的性质．
分析： 由于相似三角形的对应中线和周长的比都等于相似比，由此可求出两三角形的周长比．
解答： 解：∵△ABC与△DEF相似且对应中线的比为2：3，
∴它们的相似比为2：3；
故△ABC与△DEF的周长比为2：3．
点评： 此题主要考查了相似三角形的性质：相似三角形的一切对应线段（包括对应边、对应中线、对应高、对应角平分线等）的比等于相似比；相似三角形的周长比等于相似比．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
= 
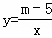（m为常数）图象的一支．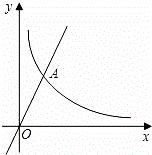
=
×
C． （3a2）3=9a6 D． 
+
=3