题目内容
如图,以▱ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=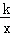 的图象交BC于D,连接AD,则四边形AOCD的面积是 .
的图象交BC于D,连接AD,则四边形AOCD的面积是 .
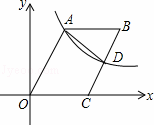
9 解:∵四边形ABCD是平行四边形,A、C的坐标分别是(2,4)、(3,0),
∴点B的坐标为:(5,4),
把点A(2,4)代入反比例函数y= 得:k=8,
得:k=8,
∴反比例函数的解析式为:y= ;
;
设直线BC的解析式为:y=kx+b,
把点B(5,4),C(3,0)代入得: ,
,
解得:k=2,b=﹣6,
∴直线BC的解析式为:y=2x﹣6,
解方程组 得:
得:
 ,或
,或  (不合题意,舍去),
(不合题意,舍去),
∴点D的坐标为:(4,2),
即D为BC的中点,
∴△ABD的面积= 平行四边形ABCD的面积,
平行四边形ABCD的面积,
∴四边形AOCD的面积=平行四边形ABCO的面积﹣△ABD的面积=3×4﹣ ×3×4=9;
×3×4=9;

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 B的平行线EF交⊙A于点F,连接AF,BF,DF.
B的平行线EF交⊙A于点F,连接AF,BF,DF.
 = .
= .




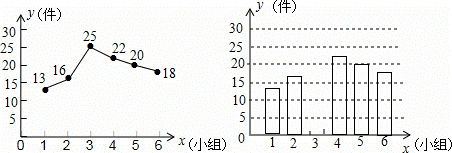
 为( )
为( ) .
. 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值可以有四个.其中正确的结论是_____________.(只填序号)