题目内容
6.过原点和M(2,2)两点画圆,分别交x轴、y轴于A、B两点,求OA+OB或OB-OA的值.分析 首先过点M作ME⊥y轴,MF⊥x轴,连接AM,BM,易证得四边形EMFO为正方形,继而可证得△AME≌△BMF,则可得AE=BF,又由OA=OE+AE,OB=OF-BF,可得OA+OB=OE+AE+OF-BF=OE+OF=2.
解答 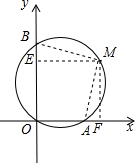 解:过点M作ME⊥y轴,MF⊥x轴,连接AM,BM,
解:过点M作ME⊥y轴,MF⊥x轴,连接AM,BM,
∵∠MEO=∠EOA=∠MFO=90°,
∴四边形EMFO为矩形,
∵M(2,2),
∴ME=MF,
∴矩形EMFO为正方形,
∵∠EOA=90°,
∴∠AMB=90°,
∴∠BME+∠EMA=90°,∠EMA+∠AMF=90°,
∴∠BME=∠AMF,
在△BME和△AMF中,
$\left\{\begin{array}{l}{∠BME=∠AMF}\\{EM=FM}\\{∠BEM=∠AFM}\end{array}\right.$,
∴△BME≌△AMF(ASA),
∴BE=AF,
∵OB=OE+BE,OA=OF-AF,
∴OA+OB=OE+BE+OF-AF=OE+OF=4.
点评 此题考查了坐标与图形的性质,圆周角定理、全等三角形的判定与性质以及正方形的性质与判定.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在平面直角坐标系中,点P在第四象限,且点P到x轴的距离是3,到y轴的距离是2,则点P的坐标为( )
| A. | (-2,3) | B. | (-3,2) | C. | (3,2) | D. | (2,-3) |
18.如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的等边三角形纸板后得到图②然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的$\frac{1}{2}$)后,得图③、④,…,记第n(n≥3)块纸板的周长为Pn,则Pn+1-Pn等于( )


| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | 3-$\frac{1}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n}}$-$\frac{1}{{2}^{n+1}}$ |
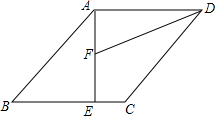 如图,已知平行四边形ABCD,AE⊥AD,AE=AD,DF平分∠ADC交AE于F,且AF=EF.若BE=3,求CE=1.
如图,已知平行四边形ABCD,AE⊥AD,AE=AD,DF平分∠ADC交AE于F,且AF=EF.若BE=3,求CE=1.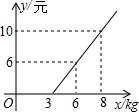 汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.
汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.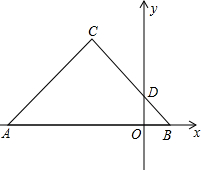 如图:等腰直角三角形ABC在平面直角坐标系中,点C坐标为(-6,8),AC=BC,∠ACB=90°,点A,B在x轴上,BC交y轴于点D,连接AD.
如图:等腰直角三角形ABC在平面直角坐标系中,点C坐标为(-6,8),AC=BC,∠ACB=90°,点A,B在x轴上,BC交y轴于点D,连接AD.