题目内容
15. 近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:方案一:整套房的单价是8000元/m2,其中厨房可免费赠送$\frac{2}{3}$的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用y1表示方案一中购买一套该户型商品房的总金额,用y2表示方案二中购买一套该户型商品房的总金额,分别求出y1、y2与x的关系式;
(2)求x取何值时,两种优惠方案的总金额一样多?
(3)张先生因现金不够,在银行借了9万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,请写张先生在借款后第n(1≤n≤72,n是正整数)个月的还款数额为P,请写出P与n之间的关系式.(用含n的式子表示)
分析 (1)根据图中线段长度,即可表示出各部分面积,进而得出两种购买方案;
(2)利用两关系式直接得出答案;
(3)①根据贷款数以及利率即可得出张先生借款后第一个月应还款数额;
②可以得出还款数额为1250+[90000-(n-1)×1250]×0.5%,进而得出即可.
解答 解:(1)∵厨房可免费赠送$\frac{2}{3}$的面积;
∴收费面积为:$\frac{1}{3}$×2×3=2,
∴y1=(18+12+$\frac{1}{3}$×6+2x)×8000
=(32+2x)×8000
=16000x+256000,
y2=(18+12+6+2x)×8000×90%
=(36+2x)×8000×0.9
=14400x+259200;
(2)令(36+2x)×0.9=32+2x,
x=2;
因此x=2时,两种优惠方案的总金额一样多;
(3)90000÷(6×12)=1250元,
1250+90000×0.5%=1250+450
=1700(元),
P=1250+[90000-(n-1)×1250]×0.5%
=1250+450-6.25(n-1)
=1700-6.25(n-1)=-6.25n+1706.25.
点评 此题主要考查了列代数式和代数式求值,根据已知正确利用每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率这些公式是解题关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
7.若代数式-a2+2a+1的值为-4,则代数式$\frac{1}{4}$a2-$\frac{1}{2}$a+5的值为( )
| A. | $\frac{25}{4}$ | B. | -$\frac{15}{4}$ | C. | $\frac{15}{4}$ | D. | 1 |
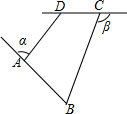 如图所示,已知四边形ABCD,∠а、∠β分别是∠BAD、∠BCD的邻补角,且∠B+∠ADC=140°,则∠а+∠β=140°.
如图所示,已知四边形ABCD,∠а、∠β分别是∠BAD、∠BCD的邻补角,且∠B+∠ADC=140°,则∠а+∠β=140°.