题目内容
6.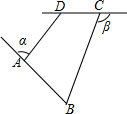 如图所示,已知四边形ABCD,∠а、∠β分别是∠BAD、∠BCD的邻补角,且∠B+∠ADC=140°,则∠а+∠β=140°.
如图所示,已知四边形ABCD,∠а、∠β分别是∠BAD、∠BCD的邻补角,且∠B+∠ADC=140°,则∠а+∠β=140°.
分析 首先根据四边形内角和可得∠DAB+∠BCD=360°-140°=220°,再根据邻补角的性质可得∠а+∠β+∠DAB+∠BCD=360°,进而得到答案.
解答 解:∵∠B+∠D+∠DAB+∠BCD=360°,∠B+∠ADC=140°,
∴∠DAB+∠BCD=360°-140°=220°,
∵∠а+∠β+∠DAB+∠BCD=360°,
∴∠а+∠β=360°-220°=140°.
故答案为:140°.
点评 此题主要考查了多边形的内角与外角,关键是掌握多边形内角和公式.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.一元二次方程x2-4x+4=0的根的情况为( )
| A. | 只有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
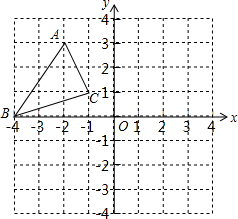 如图,已知△ABC的三个顶点在格点上.作出与△ABC关于x轴对称的△A1B1C1;写出下列点的坐标:A1(-2,-3)、
如图,已知△ABC的三个顶点在格点上.作出与△ABC关于x轴对称的△A1B1C1;写出下列点的坐标:A1(-2,-3)、 近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
近年来,随着社会竞争的日益激烈,家长为使孩子不输在教育的起跑线上,不惜花费重金购置教育质量好的学区的房产.张先生准备购买一套小户型学区房,他去某楼盘了解情况得知,该户型的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: