题目内容
 如图,弦AB与CD交于点E,已知
如图,弦AB与CD交于点E,已知 |
| CBD |
 |
| BD |
 |
| ADB |
分析:根据题意可得出
、
的度数,继而可得出∠ABD及∠BDE,在△BED中可求出∠BED的度数.
 |
| AD |
 |
| BC |
解答:
解:连接AC、CB、BD、AD,
∵
=195°,
=95°,
=215°,
∴
=
-
=120°,
=
-
=100°,
∴∠ABD=60°,∠BDE=50°,
在△BED中,可得∠BED=180°-∠ABD-∠BDE=70°.
故选A.

解:连接AC、CB、BD、AD,
∵
 |
| CBD |
 |
| BD |
 |
| ADB |
∴
 |
| AD |
 |
| ADB |
 |
| BD |
 |
| BC |
 |
| CBD |
 |
| BD |
∴∠ABD=60°,∠BDE=50°,
在△BED中,可得∠BED=180°-∠ABD-∠BDE=70°.
故选A.
点评:此题考查了圆周角定理,解答本题的关键是掌握圆周角度数等于所对应圆弧度数的一半,属于基础题,难度一般.

练习册系列答案
相关题目
 已知,如图
已知,如图 |
| BC |
 |
| AD |
| A、120° | B、100° |
| C、80° | D、60° |
 11、已知,如图弧BC与弧AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB等于( )
11、已知,如图弧BC与弧AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB等于( ) 已知,如图,弧BC与AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB=
已知,如图,弧BC与AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB= 如图,弦AB与CD交于点E,已知
如图,弦AB与CD交于点E,已知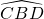 =195°,
=195°, =95°,
=95°,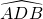 =215°,则∠BED的度数是
=215°,则∠BED的度数是