题目内容
19.某商品的进价为每件2元,当售价为每件3元时,每星期可卖出600件,当每件商品的售价每降低0.1元时,则每星期可多卖100件,设每件商品售价降价x元,每个星期的销售利润为y元.(1)当每件商品的售价降价0.5元时,求每个星期的销售利润;
(2)求y与x的函数关系式(不需要写出自变量x的取值范围);
(3)每个商品的售价定为多少元时,每个星期获得最大利润,最大的利润为多少元?
分析 (1)根据单件利润×销量=每个星期的销售利润计算即可;
(2)根据单件利润×销量=每个星期的销售利润即可求出y与x的函数关系式;
(3)由(2)求得y=1000x2+400x+600,根据顶点坐标公式即可得到结果.
解答 解:(1)根据题意得:(3-2-0.5)(600+$\frac{0.5}{0.1}$×100)=550元;
(2)根据题意得:y=(3-2-x)(600+$\frac{x}{0.1}$×100)=-1000x2+400x+600,
即:y=1000x2+400x+600,
(3)由(2)求得y=1000x2+400x+600,
当x=0.2时,y=640元;
即:每个商品的售价定为2.8元时,每个星期获得最大利润,最大的利润为640元.
点评 本题考查了二次函数的应用:根据实际问题列出二次函数关系式,再配成抛物线的顶点式y=a(x-h)2+k,然后利用当a<0,x=h时,y有最大值k;当a>0,x=h时,y有最小值k等性质解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?
某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?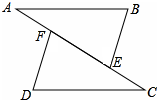 如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.
如图,点A、F、E、C在同一条直线上,AF=CE,BE=DF,AB=CD,求证:AB∥CD.