题目内容
如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．（1）求A′点的坐标；
（2）求过C，A′，A三点的抛物线y=ax2+bx+c的解析式．
【答案】分析：（1）由题意可知，∠A′OA的度数和旋转角的度数相同，可过A′作x轴的垂线，在构建的直角三角形中可根据OA′的长和∠A′OA的度数求出A′的坐标；
（2）根据C，A′，A三点的坐标，可用待定系数法求出抛物线的解析式．
解答：
解：（1）过点A′作A′D垂直于x轴，垂足为D，则四边形OB′A′D为矩形．
在△A′DO中，∵A′D=OA′•sin∠A′OD=4×sin60°=2
，
OD=A′B′=AB=2，
∴点A′的坐标为（2，2
）；
（2）∵C（0，4）在抛物线上，
∴c=4，
∴y=ax2+bx+4，
∵A（4，0），A′（2，2
）在抛物线y=ax2+bx+4上，
∴
，
解得，
，
故所求抛物线的解析式为：y=
x2+（2
-3）x+4．
点评：本题考查的是二次函数综合题，涉及到用待定系数法求二次函数解析式、图形旋转变换等知识点，难度不大．
（2）根据C，A′，A三点的坐标，可用待定系数法求出抛物线的解析式．
解答：
解：（1）过点A′作A′D垂直于x轴，垂足为D，则四边形OB′A′D为矩形．在△A′DO中，∵A′D=OA′•sin∠A′OD=4×sin60°=2
，OD=A′B′=AB=2，
∴点A′的坐标为（2，2
）；（2）∵C（0，4）在抛物线上，
∴c=4，
∴y=ax2+bx+4，
∵A（4，0），A′（2，2
）在抛物线y=ax2+bx+4上，∴
，解得，
，故所求抛物线的解析式为：y=
x2+（2-3）x+4．点评：本题考查的是二次函数综合题，涉及到用待定系数法求二次函数解析式、图形旋转变换等知识点，难度不大．
练习册系列答案
相关题目
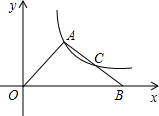（2012•泸州）如图，在△OAB中，C是AB的中点，反比例函数y=
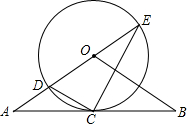如图，在△OAB中，OA=OB，以点O为圆心的⊙0经过AB的中点C，直线AO与⊙0相交于点D、E，连接CD、CE．
如图，在△OAB中，C是AB的中点，反比例函数y=
如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．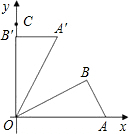
（创新学习）如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．