题目内容
 如图,点E是Rt△ABC斜边AB的中点,△ADE是以E为直角顶点的等腰直角三角形,DE与AC交于点F,连接CD.若BC=CD,AB=2,则△ADF的面积为( )
如图,点E是Rt△ABC斜边AB的中点,△ADE是以E为直角顶点的等腰直角三角形,DE与AC交于点F,连接CD.若BC=CD,AB=2,则△ADF的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的判定与性质,等腰直角三角形
专题:
分析:根据直角三角形斜边上的中线等于斜边的一半得到AE=BE=CE=
AB=1,再根据等腰直角三角形的性质得AE=DE=1,AD=
AE=
,∠DAE=45°,
则可根据“SSS”判断△EBC≌△EDC,所以∠BEC=∠DEC=45°,于是EC∥AD,所以△ECF∽△DAF,根据相似的性质得
=
=
,利用比例性质可得到DF=2-
,然后根据三角形面积公式计算即可.
| 1 |
| 2 |
| 2 |
| 2 |
则可根据“SSS”判断△EBC≌△EDC,所以∠BEC=∠DEC=45°,于是EC∥AD,所以△ECF∽△DAF,根据相似的性质得
| EF |
| FD |
| EC |
| AD |
| 1 | ||
|
| 2 |
解答:解:连结CE,如图,
∵点E是Rt△ABC斜边AB的中点,
∴AE=BE=CE=
AB=1,
∵△ADE是等腰直角三角形,
∴AE=DE=1,AD=
AE=
,∠DAE=45°,
∴ED=EC=EB,
而BC=CD,
∴△EBC≌△EDC,
∴∠BEC=∠DEC,
而∠BED=90°,
∴∠BEC=45°,
∴∠BEC=∠DAE,
∴EC∥AD,
∴△ECF∽△DAF,
∴
=
=
,
∴
=
,即
=
,
∴DF=2-
,
∴△ADF的面积=
AE•DF=
×1×(2-
)=
.
故选A.

∵点E是Rt△ABC斜边AB的中点,
∴AE=BE=CE=
| 1 |
| 2 |
∵△ADE是等腰直角三角形,
∴AE=DE=1,AD=
| 2 |
| 2 |
∴ED=EC=EB,
而BC=CD,
∴△EBC≌△EDC,
∴∠BEC=∠DEC,
而∠BED=90°,
∴∠BEC=45°,
∴∠BEC=∠DAE,
∴EC∥AD,
∴△ECF∽△DAF,
∴
| EF |
| FD |
| EC |
| AD |
| 1 | ||
|
∴
| DF+EF |
| DF |
| ||
|
| 1 |
| DF |
| ||
|
∴DF=2-
| 2 |
∴△ADF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
2-
| ||
| 2 |
故选A.
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线与其他两边所截得的三角形与原三角形相似;相似三角形的对应角相等,对应边的比相等.也考查了全等三角形的判定与性质以及等腰直角三角形的性质.

练习册系列答案
相关题目
 如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为( )
如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为( )A、4
| ||
B、2
| ||
C、
| ||
| D、无法确定 |
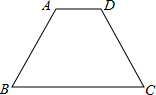 如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=3,BC=7,则梯形ABCD的腰长AB=
如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=3,BC=7,则梯形ABCD的腰长AB= 如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,-3)、B(-4,0).
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,-3)、B(-4,0). 王老师在讲实数时,画了图(如图所示).即“以数轴的单位长线段为边作一个正方形,然后以点O为圆心,以正方形的对角线长为半径画弧交数轴上一点A”,则点A表示的数是
王老师在讲实数时,画了图(如图所示).即“以数轴的单位长线段为边作一个正方形,然后以点O为圆心,以正方形的对角线长为半径画弧交数轴上一点A”,则点A表示的数是