题目内容
4.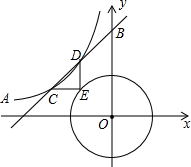 如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.
如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.
分析 作CM⊥x轴于点M,EG⊥x轴于点G.连接OG,则△CFM和△OGE都是等腰直角三角形,证明FC=CD=BD,根据△FCM∽△FBO,求得C的坐标,然后利用待定系数法求得k的值.
解答  解:∵y=x+3$\sqrt{2}$中,令y=0,解得:x=3$\sqrt{2}$,
解:∵y=x+3$\sqrt{2}$中,令y=0,解得:x=3$\sqrt{2}$,
令x=0,解得:y=3$\sqrt{2}$,
∴OF=OB,即△OBF是等腰直角三角形.
作CM⊥x轴于点M,EG⊥x轴于点G.连接OG.
则△CFM和△OGE都是等腰直角三角形.
又∵CD=OE,
∴CM=OG=EG=CM,
∴CF=CD.
同理,FC=CD=BD.
∵CM∥OB,
∴△FCM∽△FBO,
∴$\frac{FM}{OF}$=$\frac{CM}{OB}$=$\frac{FC}{BF}$=$\frac{1}{3}$.
∴FM=$\frac{1}{3}$OF=$\sqrt{2}$,CM=$\frac{1}{3}$OB=$\sqrt{2}$,
∴OM=2$\sqrt{2}$,
∴C的坐标是(-2$\sqrt{2}$,$\sqrt{2}$).
把C代入y=$\frac{k}{x}$,得:k=-4.
点评 本题考查了待定系数法求函数的解析式,以及相似三角形的判定与性质,正确证明FC=CD=BD是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
9.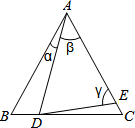 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )| A. | 当∠β为定值时,∠CDE为定值 | B. | 当∠α为定值时,∠CDE为定值 | ||
| C. | 当∠γ为定值时,∠CDE为定值 | D. | ∠CDE的值与∠α,∠β,∠γ的值无关 |
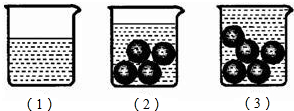
16.如图是测量一颗玻璃球体积的过程:
(1)将60ml的水倒进一个容量为100ml的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在( )(1ml=1cm3)
(1)将60ml的水倒进一个容量为100ml的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在( )(1ml=1cm3)

| A. | 6cm3以上,8cm3以下 | B. | 8cm3以上,10cm3以下 | ||
| C. | 10cm3以上,12cm3以下 | D. | 12cm3以上,14cm3以下 |
13.-5的相反数是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |